红黑树概念

红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

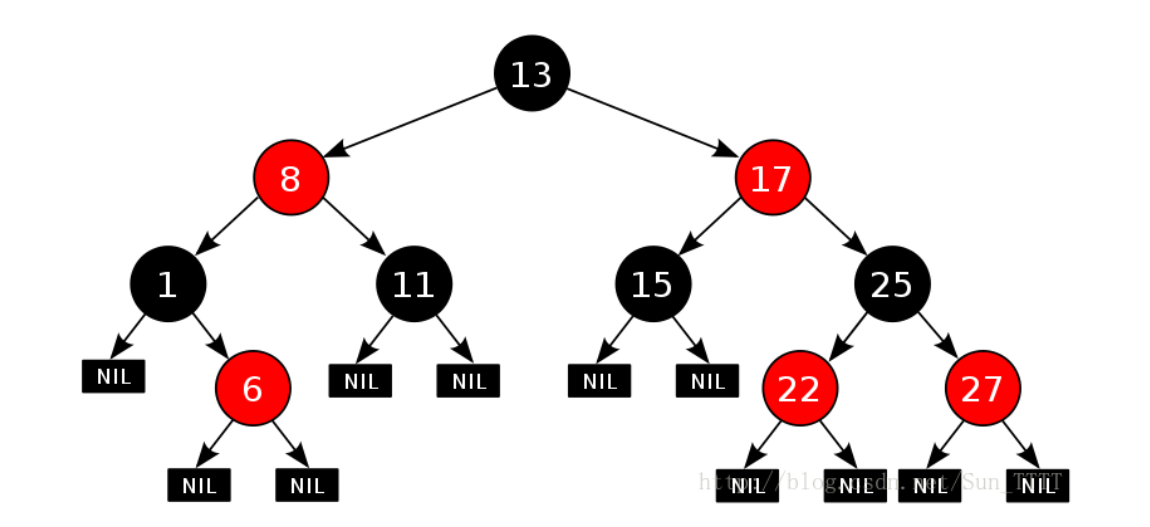
红黑树的性质

  1. 每个结点不是红色就是黑色
  2. 根节点是黑色的
  3. 如果一个节点是红色的，则它的两个孩子结点是黑色的，树中没有连续的红节点
  4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点
  5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

为什么满足上面的性质，红黑树就能保证：其最长路径中节点个数不会超过最短路径中节点个数的两倍？

极限最短：全黑
极限最长：一黑一红

红黑树结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
enum Color
{
    RED,
    BLACK
};

template <class K, class V>
struct RBTreeNode
{
    RBTreeNode<K, V> *_parent;
    RBTreeNode<K, V> *_left;
    RBTreeNode<K, V> *_right;
    pair<K, V> _kv;
    Color _col;

    RBTreeNode(const pair<K, V> &kv)
        : _parent(nullptr), _left(nullptr), _right(nullptr), _kv(kv), _col(RED)
    {
    }
};

template <class K, class V>
class RBTree
{
    typedef RBTreeNode<K, V> Node;

public:
    bool insert(const pair<K, V> &kv)
    {
    }
private:
    Node *_root = nullptr;
};

红黑树操作

插入

红黑树的叔叔是关键
u存在且为红，变色继续向上处理
u不存在或存在且为黑，旋转（单旋+双旋）+变色

情况一：cur为红，parent为红，grandfather为黑（固定），uncle存在且为红

处理：p、u变黑，g变红，继续把g当成cur

  • g不是根，往上继续处理
  • g是根，再把g变成黑色

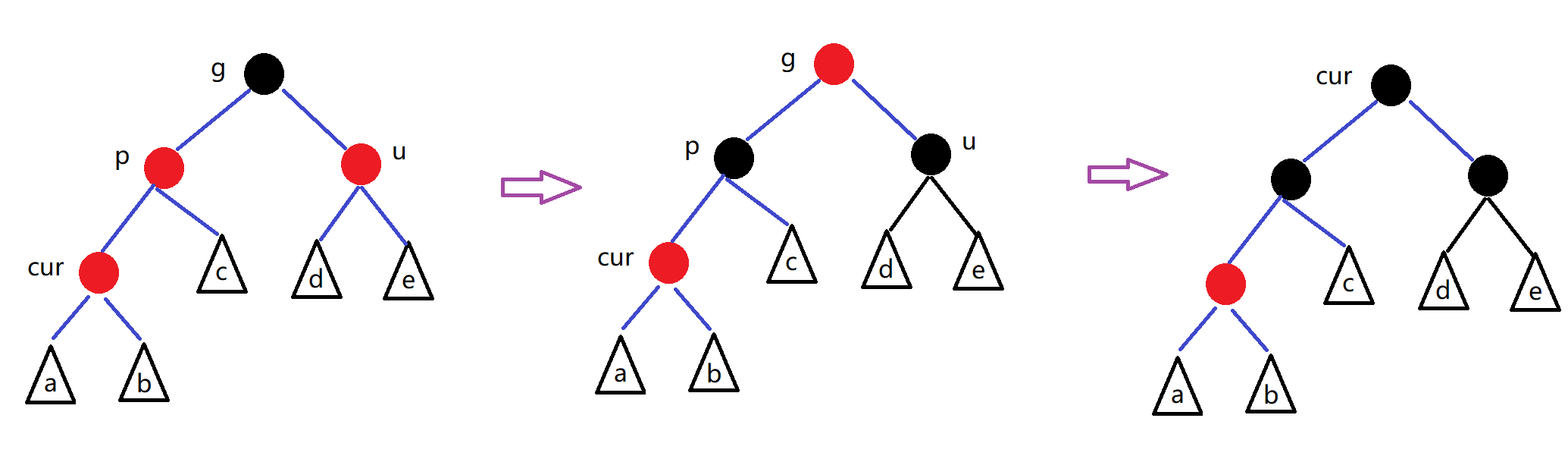
情况二：cur为红，parent为红，grandfather为黑（固定），u不存在/u存在且为黑（单旋+变色）

处理：

  • g右单旋
  • p变黑，g变红

说明：uncle的情况有两种

  • 如果u节点不存在，那么cur一定是新插入节点，因为如果cur不是新插入节点，则cur和p一定有个节点颜色是黑色，就不满足性质4：每条路径黑色节点的个数相同。
  • 如果u节点存在，那么cur节点原来的颜色一定是黑色的（保证性质4），现在看到其是红色的原因是因为cur的子树在调整的过程中将cur节点的颜色由黑色改为红色。

u不存在

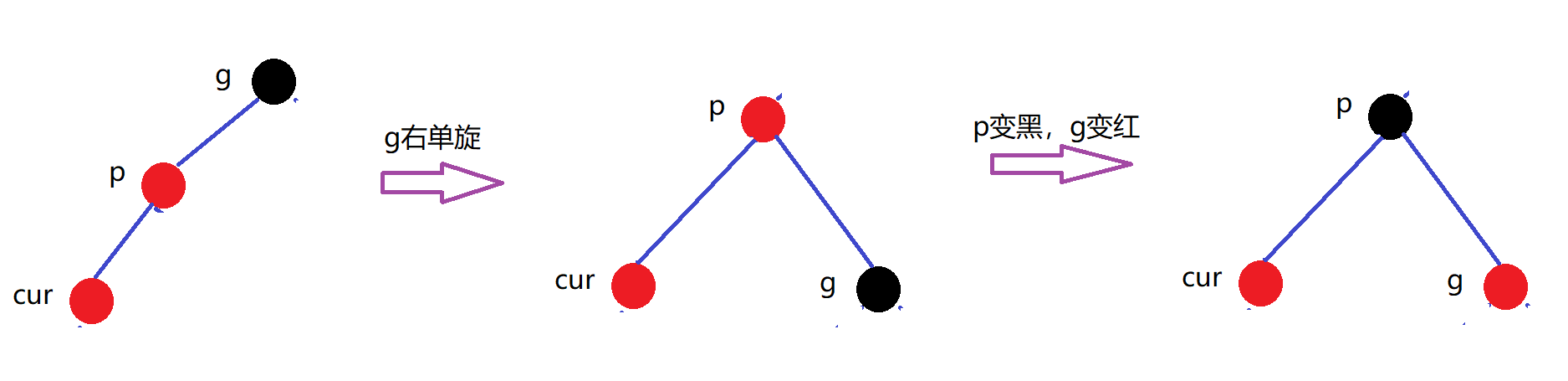
u存在且为黑

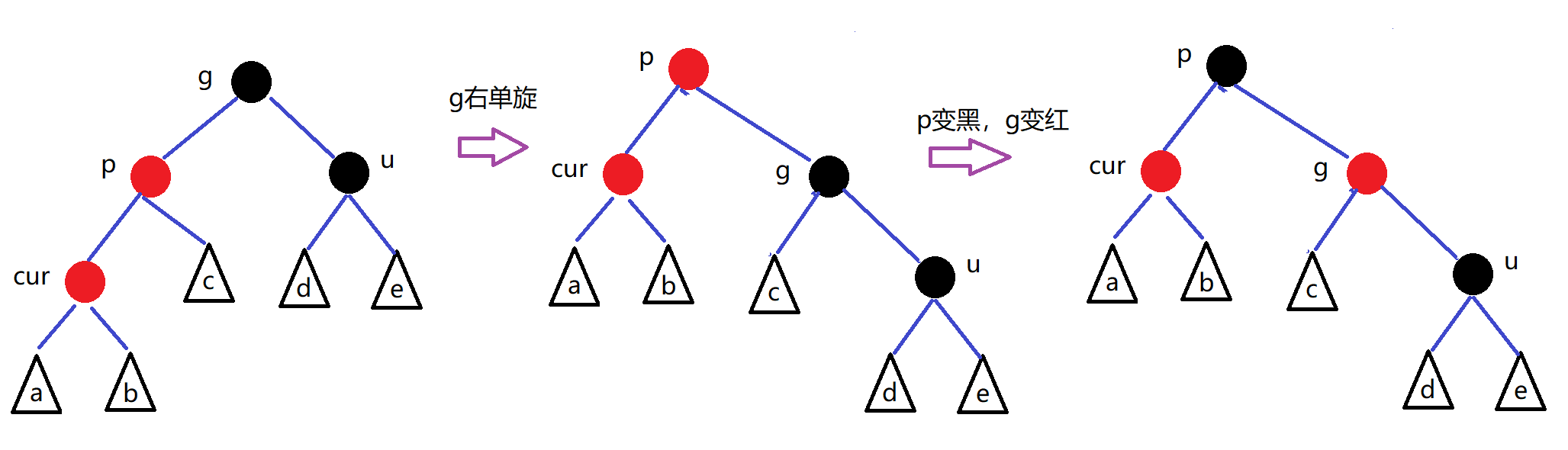
情况三：cur为红，parent为红，grandfather为黑（固定），u不存在/u存在且为黑（双旋+变色）

u不存在

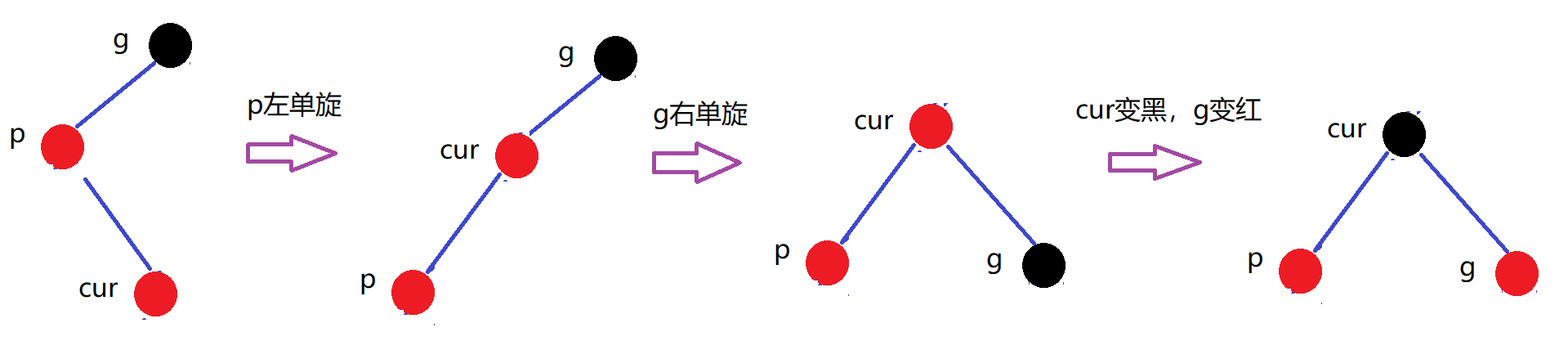
u存在且为黑

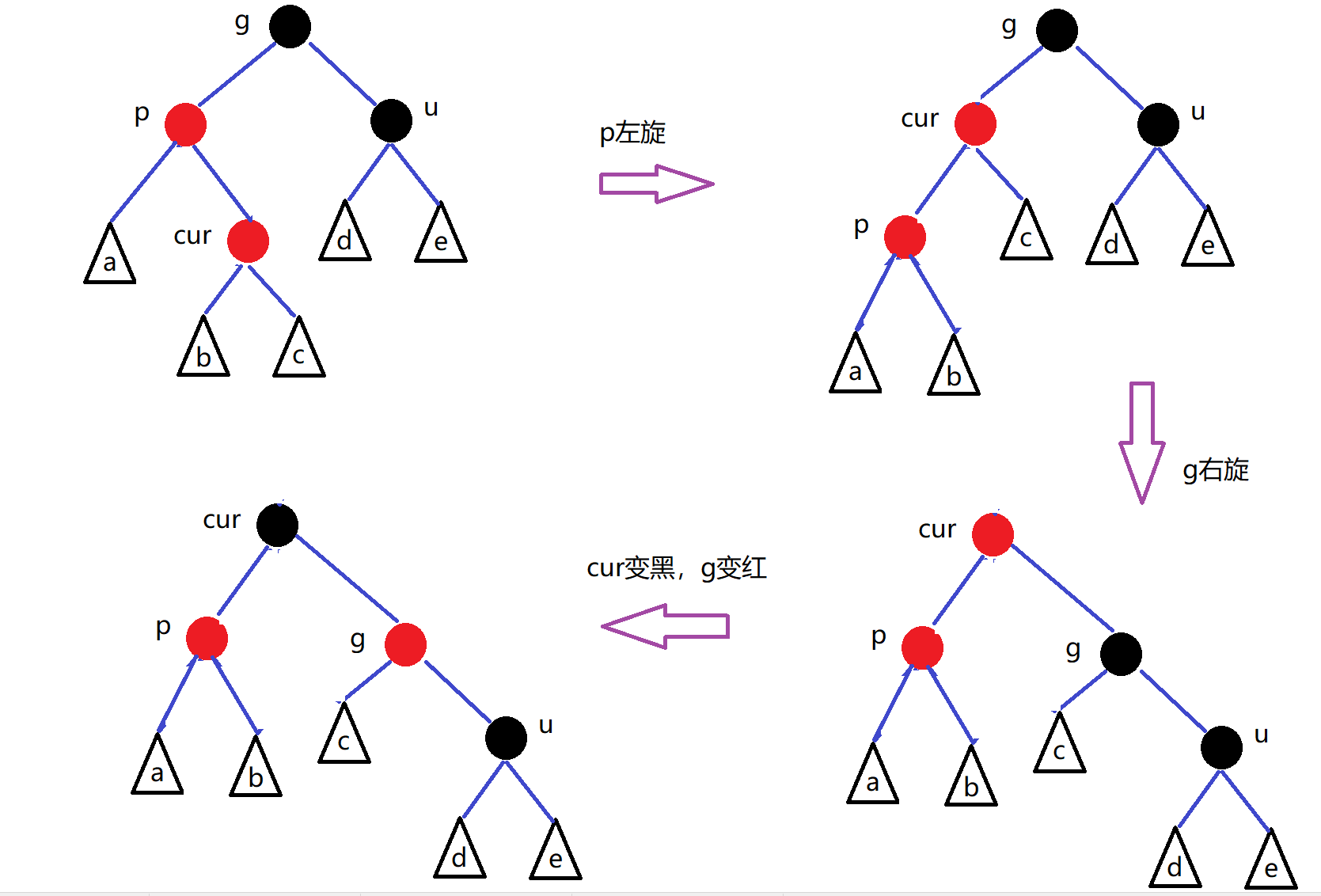
插入代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
bool insert(const pair<K, V> &kv)
{
	if (_root == nullptr)
	{
		_root = new Node(kv);
		_root->_col = BLACK;
		return true;
	}

	Node *parent = nullptr;
	Node *cur = _root;
	while (cur)
	{
		if (cur->_kv.first < kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_kv.first > kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}

	cur = new Node(kv);
	// 还得链接上
	if (parent->_kv.first < kv.first)
	{
		parent->_right = cur;
	}
	else
	{
		parent->_left = cur;
	}
	cur->_parent = parent;

	// 找到了应该插入的位置
	while (parent && parent->_col == RED) // parent不为空并且颜色为红继续处理
	{
		Node *grandfather = parent->_parent;
		// 如果父亲存在且颜色为红，那么祖父一定存在颜色为黑
		assert(grandfather);
		assert(grandfather->_col = BLACK);

		// 先看parent是grandfather的左还是右
		if (parent == grandfather->_left)
		{
			Node *uncle = grandfather->_right;

			// 情况1、叔叔存在且为红，变色继续向上处理
			if (uncle && uncle->_col == RED)
			{
				parent->_col = uncle->_col = BLACK;
				grandfather->_col = RED;

				// 继续向上处理
				cur = grandfather;
				parent = cur->_parent;
			}
			else // 情况2、3：uncle不存在  存在且为黑
			{
				// 分两种
				// 1、右单旋+变色
				//     g
				//   p   u
				// c
				if (cur == parent->_left)
				{
					RotateR(grandfather);
					parent->_col = BLACK;
					grandfather->_col = RED;
				}
				else
				{
					// 先对p 左单旋，再对g 右单旋，最后变色
					//     g
					//   p   u
					//     c
					RotateL(parent);
					RotateR(grandfather);
					cur->_col = BLACK;
					grandfather->_col = RED;
				}
				break;
			}
		}
		else // parent=grand->right
		{
			Node *grandfather = parent->_parent;
			// 如果父亲存在且颜色为红，那么祖父一定存在颜色为黑
			assert(grandfather);
			assert(grandfather->_col = BLACK);

			Node *uncle = grandfather->_left;

			// 情况1、叔叔存在且为红，变色继续向上处理
			if (uncle && uncle->_col == RED)
			{
				parent->_col = uncle->_col = BLACK;
				grandfather->_col = RED;

				// 继续向上处理
				cur = grandfather;
				parent = cur->_parent;
			}
			else // 情况2、3：uncle不存在  存在且为黑
			{
				// 分两种
				//     g
				//   u   p
				//         c
				if (cur == parent->_right)
				{
					RotateL(grandfather);
					parent->_col = BLACK;
					grandfather->_col = RED;
				}
				else
				{
					//     g
					//   u   p
					//     c
					RotateR(parent);
					RotateL(grandfather);
					cur->_col = BLACK;
					grandfather->_col = RED;
				}
				break;
			}
		}
	}
	_root->_col = BLACK;
	return true;
}

检查

  • 根是黑色
  • 没有连续的红节点
  • 每条路径的黑色节点数量相同
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
bool is_balance()
{
	if (_root == nullptr)
	{
		return true;
	}

	if (_root->_col == RED)
	{
		cout << "根节点不是黑色" << endl;
		return false;
	}
	int bench_mark = 0;

	return prev_check(_root, 0, bench_mark);
}

bool prev_check(Node *root, int bnum, int &bench_mark)
{
	if (root == nullptr)
	{
		if (bench_mark == 0)
		{
			bench_mark = bnum;
			return true;
		}
	
		if (bench_mark != bnum)
		{
			cout << "某条黑色节点的数量不相等" << endl;
			return false;
		}
		else
		{
			return true;
		}
	}
	
	if (root->_col == BLACK)
	{
		++bnum;
	}
	
	if (root->_col == RED && root->_parent->_col == RED)
	{
		cout << "存在连续的红色节点" << endl;
		return false;
	}
	
	return prev_check(root->_left, bnum, bench_mark) && prev_check(root->_right, bnum, bench_mark);
}