AVL概念

当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：

  • 它的左右子树都是AVL树
  • 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在
O(log2n)O(log_2 n)，搜索时间复杂度O(log2nlog_2 n)

AVL操作

插入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
bool insert(const pair<K, V> &kv)
{
	if (_root == nullptr)
	{
		_root = new Node(kv);
		return true;
	}

	Node *parent = nullptr;
	Node *cur = _root;
	while (cur)
	{
		// 插入先找位置
		if (cur->_kv.first > kv.first)
		{
			// 先记录parent
			parent = cur;
			// 插入的比当前值小，往左边走
			cur = cur->_left;
		}
		else if (cur->_kv.first < kv.first)
		{
			parent = cur;
			// 插入值比左边大，往右边走
			cur = cur->_right;
		}
		else
		{
			// 相等的位置
			return false;
		}
	}

	// 走到这里cur为空，说明，找到了该插入的位置
	cur = new Node(kv);
	// 链接
	if (parent->_kv.first > kv.first)
	{
		parent->_left = cur;
	}
	else
	{
		parent->_right = cur;
	}
	cur->_parent = parent;

	// 插入成功。现在需要控制平衡，更新平衡因子
	// 向上更新直到parent为空
	while (parent)
	{
		if (parent->_left == cur)
		{
			parent->_bf--;
		}
		else
		{
			parent->_bf++;
		}

		if (parent->_bf == 0)
		{
			break;
		}
		// else if(parent->_bf==1 || parent->_bf==-1)
		else if (abs(parent->_bf) == 1)
		{
			// cur = parent;
			// parent = parent->_parent;
			parent = parent->_parent;
			cur = cur->_parent;
		}
		else if (abs(parent->_bf) == 2)
		{
			if (parent->_bf == 2 && cur->_bf == 1)
			{
				// 左单旋
				RotateL(parent);
			}
			else if (parent->_bf == -2 && cur->_bf == -1)
			{
				// 右单旋
				RotateR(parent);
			}
			else if (parent->_bf == 2 && cur->_bf == -1)
			{
				// 右左旋
				RotateRL(parent);
			}
			else if (parent->_bf == -2 && cur->_bf == 1)
			{
				// 左右旋
				RotateLR(parent);
			}
			else
			{
				assert(false);
			}

			// 调整完成之后break;
			break;
		}
		else
		{
			assert(false);
		}
	}
	return true;
}

判断平衡

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
bool is_balance()
{
	return _is_balance(_root);
}


int get_height(Node *root)
{
	if (root == nullptr)
		return 0;

	int left = get_height(root->_left);
	int right = get_height(root->_right);

	return max(left, right) + 1;
}

bool _is_balance(Node *root)
{
	if (root == nullptr)
	{
		return true;
	}

	int left = get_height(root->_left);
	int right = get_height(root->_right);

	int diff = right-left;
	if (diff != root->_bf)
	{
		cout << root->_kv.first << " 平衡因子异常" << endl;
		return false;
	}
	return abs(diff) < 2 && _is_balance(root->_left) && _is_balance(root->_right);
	// if(abs(left-right)>=2)
	// {
	//     return false;
	// }
}

平衡因子更新

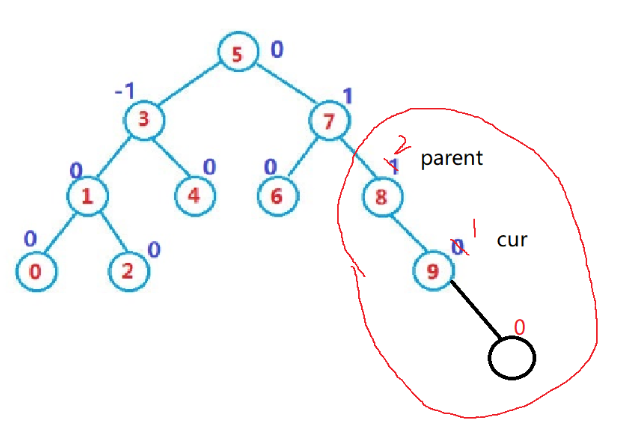
更新平衡因子的规则

  • 新增在右，parent->bf++，新增在左，parent->bf–
  • 更新后，parent->bf == 1 or -1, 说明parent插入前的平衡因子是0，说明左右子树高度相等，插入后有一边高，parent高度变了，需要继续往上更新
  • 更新后，parent->bf == 0，说明parent插入前的平衡因子是1 or -1， 说明左右子树一边高一边低，插入后两边一样高，插入填上了矮的那边，parent所在子树高度不变，不需要往上更新
  • 更新后，parent->bf == 2 or -2 ，说明parent插入前的平衡因子是1 or -1，已经平衡临界值，插入后变成2 or -2，打破平衡，parent所在子树需要旋转处理
  • 更新后，parent->bf >2 or < -2，不可能，如果存在，则说明插入前就不是AVL树，需要去检查之前操作的问题

旋转的场景

旋转的价值和意义：

  • 平衡
  • 降低高度（高度恢复到插入之前的样子）

左单旋

情景分析

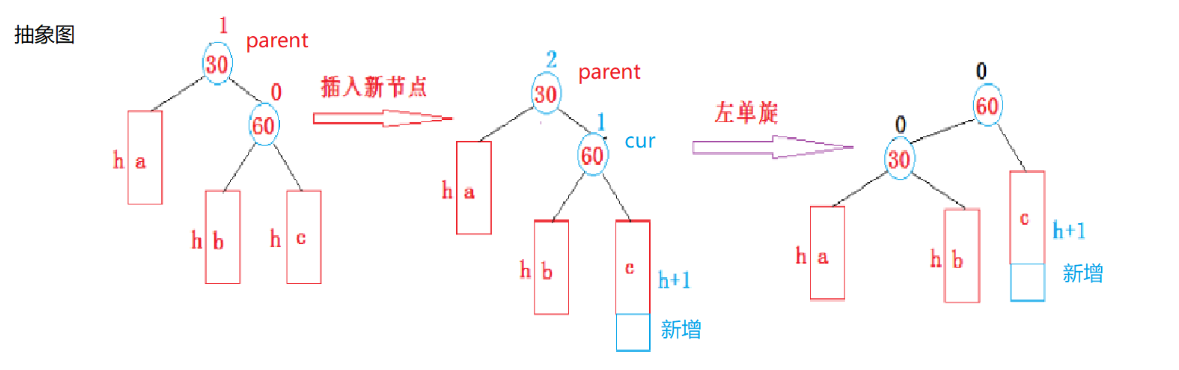
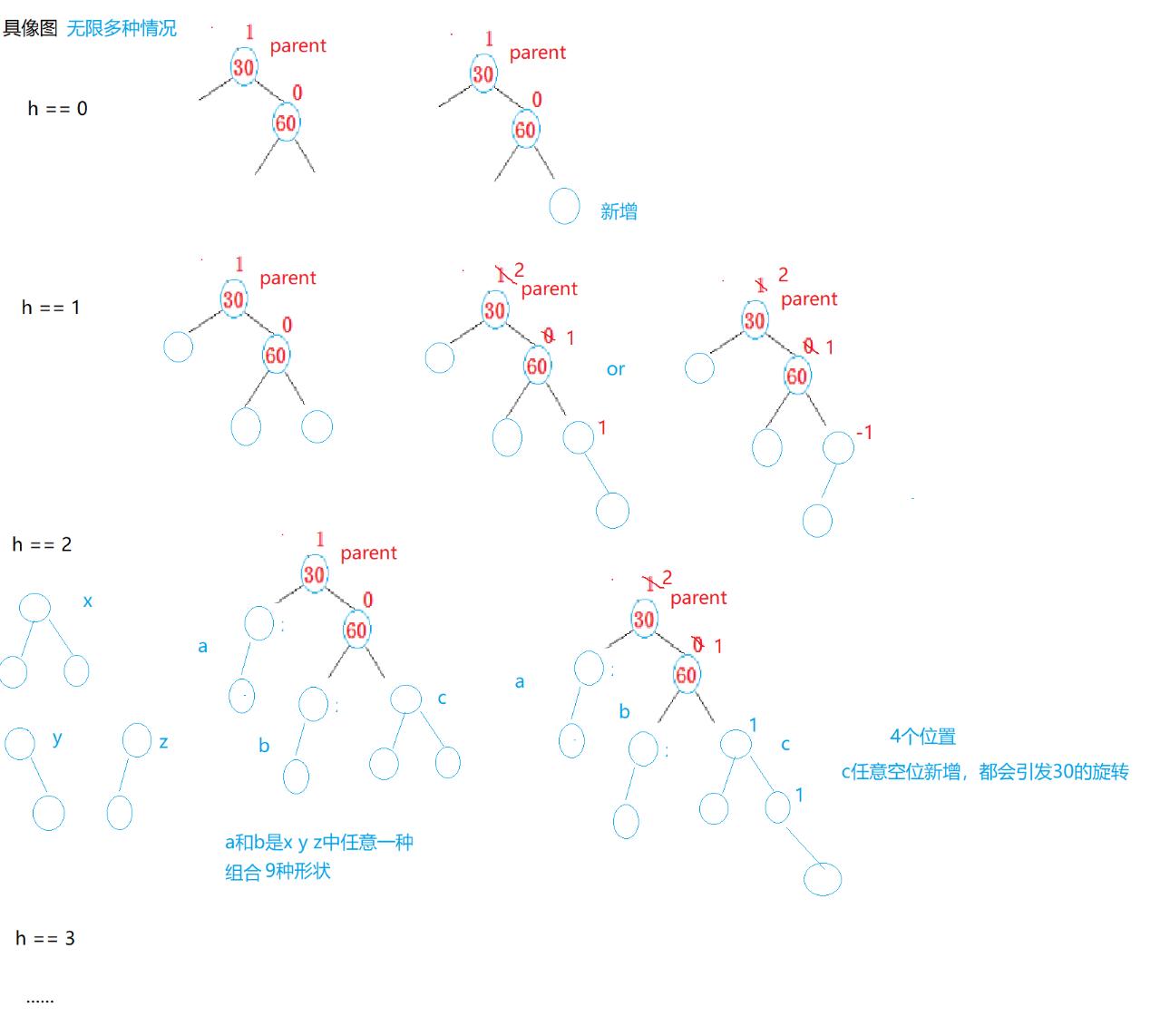
具体进行左旋的时候也要分两种情况

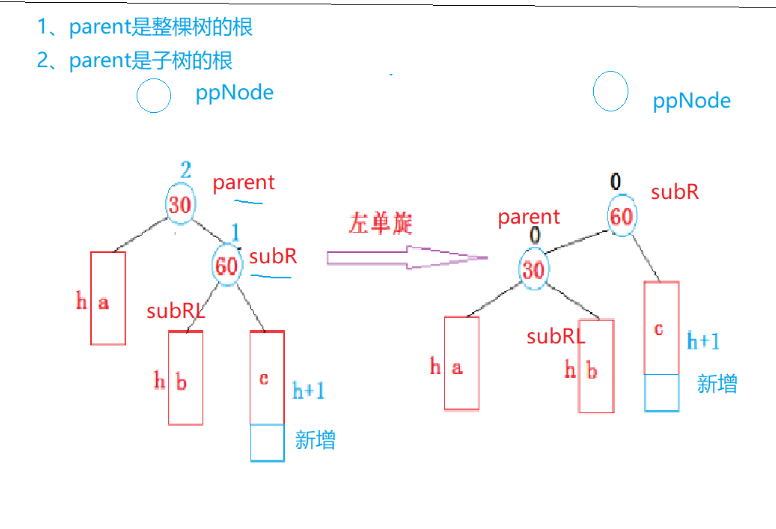
调整完成之后，parent的平衡因子变为0，subR变为新的根，同时平衡因子也变为0

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 左单旋
void RotateL(Node* parent)
{
	//右边高
	Node *subR = parent->_right;
	Node *subRL = subR->_left;

	parent->_right = subRL;
	if(subRL)
	{
		subRL->_parent = parent;
	}

	Node *ppNode = parent->_parent;
	subR->_left = parent;

	if(parent==_root)
	{
		_root = subR;
		subR->_parent = nullptr;
	}
	else
	{
		if(ppNode->_left=parent)
		{
			ppNode->_left = subR;
		}
		else
		{
			ppNode->_right = subR;
		}

		subR->_parent = ppNode;
	}
}

右单旋

情景分析‘

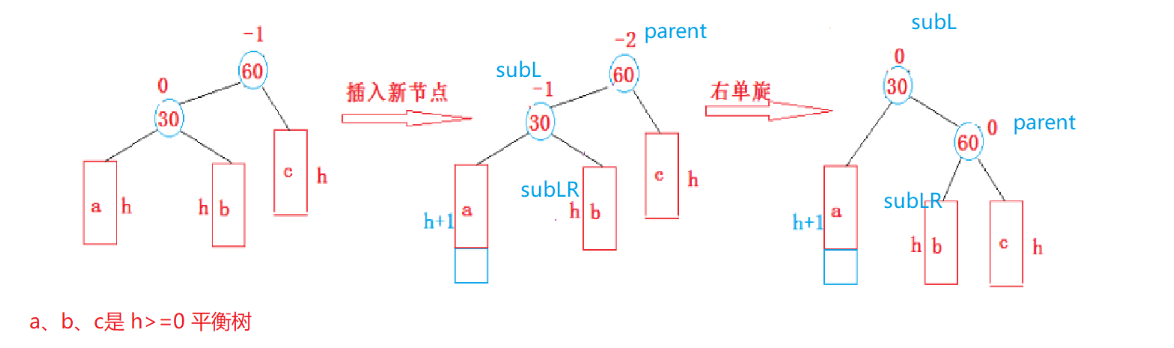
代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
  //右单旋
void RotateR(Node* parent)
{
	//左边高
	Node* subL = parent->_left;
	Node *subLR = subL->_right;

	//先记录一些parent的父亲
	Node *ppNode = parent->_parent;

	//让subL的右给parent的左，然后parent做subL的右，subL做新的根
	parent->_left = subLR;
	// 注意 要判断subLR是不是空
	if(subLR)
	{
		subLR->_parent = parent;
	}

	subL->_right = parent;
	parent->_parent = subL;

	// 这里也注意,
	if(_root==parent)
	{
		_root = subL;
		subL->_parent = nullptr;
	}
	else
	{
		if (ppNode->_left == parent)
		{
			ppNode->_left = subL;
		}
		else
		{
			ppNode->_right = subL;
		}

		//然后让suL的parent指向ppNode
		subL->_parent = ppNode;
	}
	

	subL->_bf = 0;
	parent->_bf = 0;
}

左右旋

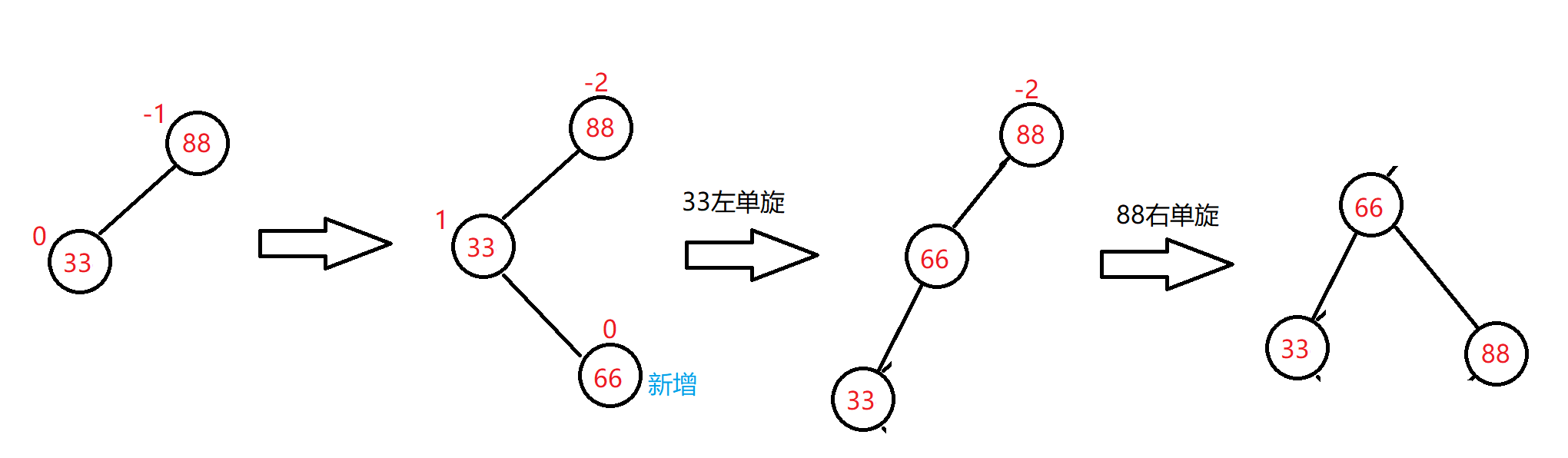
情景分析

三种情况：

1、在b新增，那么60节点的平衡因子是-1
2、在c新增，那么60节点的平衡因子是1

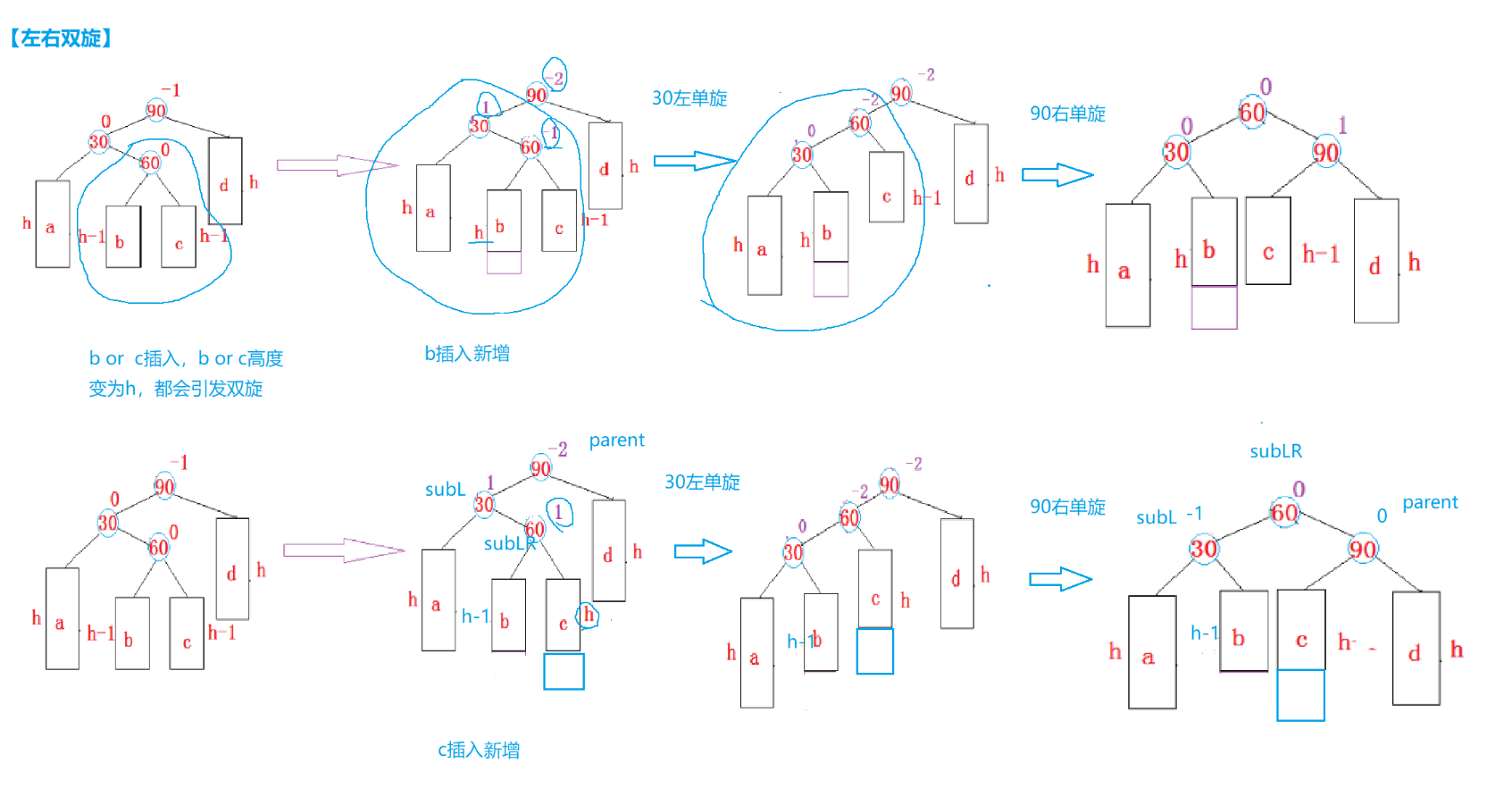
3、subLR就是新增

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// 左右旋
void RotateLR(Node *parent)
{
	Node *subL = parent->_left;
	Node *subLR = subL->_right;
	int bf = subLR->_bf;

	RotateL(parent->_left);
	RotateR(parent);

	// 注意，subLR变成新的根
	subLR->_bf = 0;

	if (bf == -1)
	{
		// 在b插入
		parent->_bf = 1;
		subL->_bf = 0;
	}
	else if (bf == 0)
	{
		// subLR就是新增
		parent->_bf = 0;
		subL->_bf = 0;
	}
	else if (bf == 1)
	{
		// 在c插入
		parent->_bf = 0;
		subL->_bf = -1;
	}
	else
	{
		assert(false);
	}
}

右左旋

情景分析

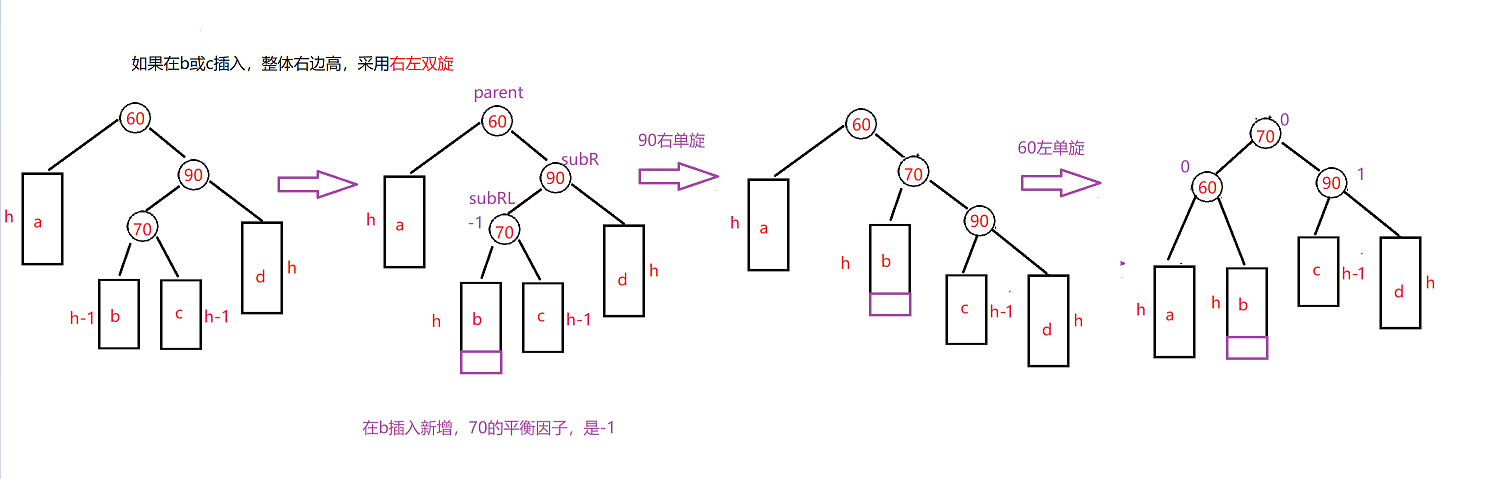
1、新增在b，那么subRL平衡因子变成-1，先对subR进行右旋，然后再对parent进行左旋，调整完成之后，subRL也就是70节点变成了根，平衡因子为0，parent的平衡因子为0，subR就是90的平衡因子变成1.

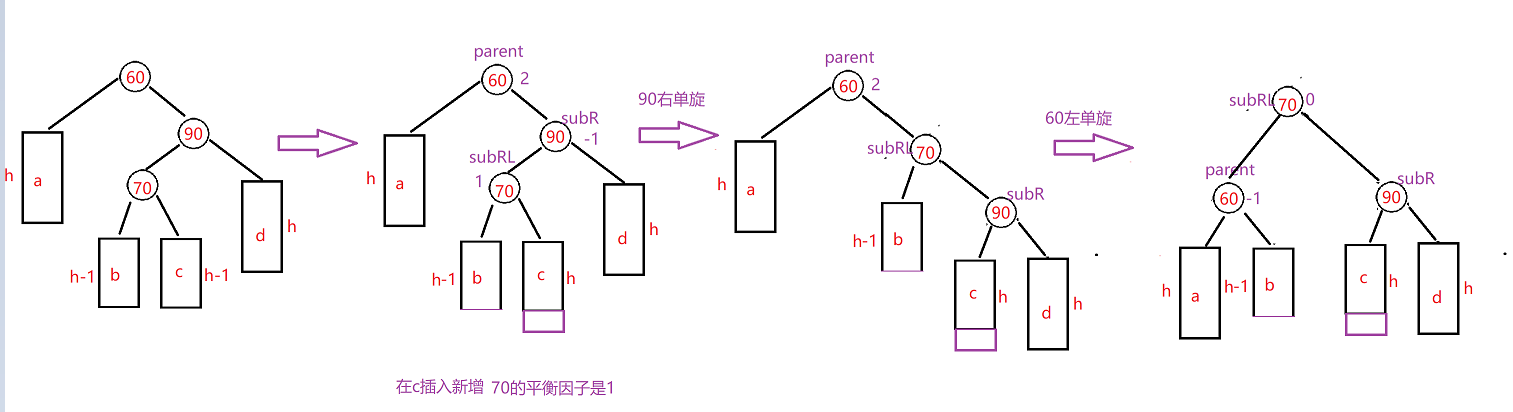
2、新增在c，那么subRL平衡因子变成1，先对subR进行右旋，然后再对parent进行左旋，调整完成之后，subRL也就是70节点变成了根，平衡因子为0，parent的平衡因子为-1，subR就是90的平衡因子变成0。

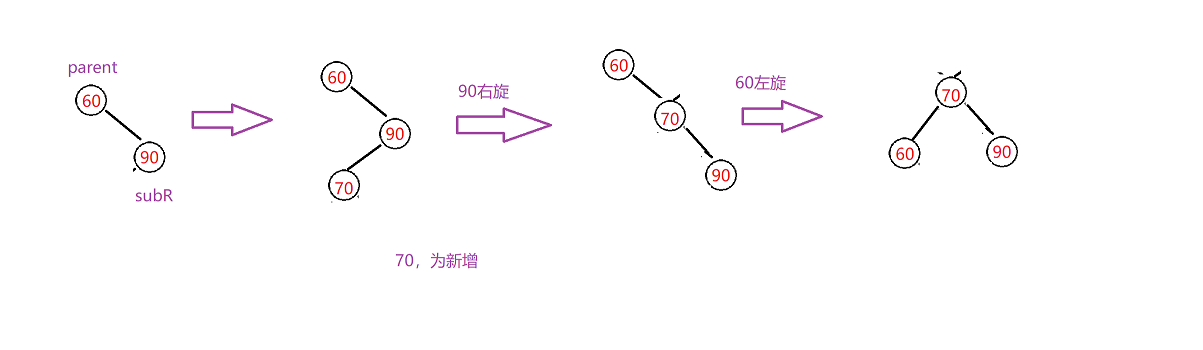
3、新增就是subRL，subRL平衡因子为0，调整完成后都是0

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
// 右左旋
void RotateRL(Node *parent)
{
	Node *subR = parent->_right;
	Node *subRL = subR->_left;
	int bf = subRL->_bf;

	RotateR(subR);
	RotateL(parent);

	subRL->_bf = 0;

	// 判断subRL的平衡因子是多少
	if (bf == -1)
	{
		subR->_bf = 1;
		parent->_bf = 0;
	}
	else if (bf == 0)
	{
		parent->_bf = 0;
		subR->_bf = 0;
	}
	else if (bf == 1)
	{
		parent->_bf = -1;
		subR->_bf = 0;
	}
	else
	{
		assert(false);
	}
}