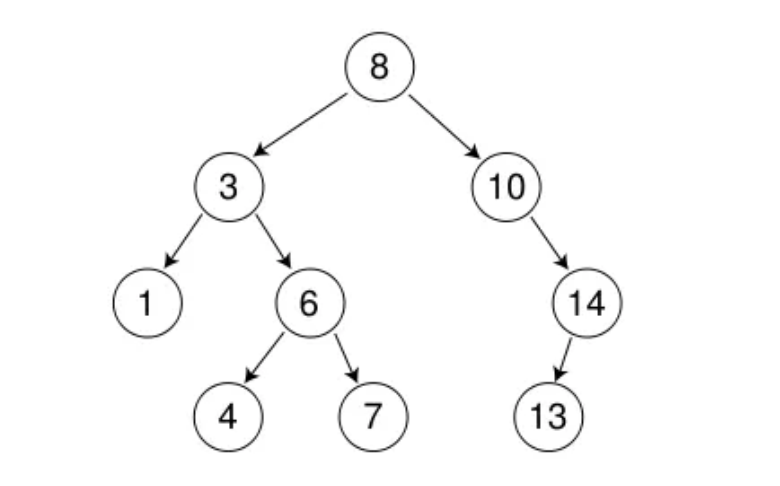
二叉搜索树概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
二叉搜索树实现
结构框架
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| template <class K>
struct BSTreeNode
{
BSTreeNode *left;
BSTreeNode *right;
K _key;
BSTreeNode(const K &key) : left(nullptr), right(nullptr), _key(key){};
};
template <class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
private:
Node *_root = nullptr;
};
|
构造
让编译器提供个默认生成的就可以了,如果不写这个,又写了拷贝构造,编译器就不会自己自动生成了。
拷贝构造
递归拷贝左,右,根
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
BSTree(const BSTree<K> &t)
{
_root = _copy(t._root);
}
Node *_copy(Node *root)
{
if (root == nullptr)
{
return nullptr;
}
Node *node = new Node(root->_key);
node->left = _copy(root->left);
node->right = _copy(root->right);
return node;
}
|
赋值运算符重载
写完拷贝构造之后可以直接用现在写法就OK了
1
2
3
4
5
6
| BSTree<K> operator=(BSTree<K> t)
{
std::swap(_root, t._root);
return *this;
}
|
析构
递归,左、右、根
1
2
3
4
5
6
7
8
9
| void _destory(Node *&root)
{
if (root == nullptr)
return;
_destory(root->left);
_destory(root->right);
delete root;
root = nullptr;
}
|
插入
比它大往右走,比他小往左走,走到空,找它父亲链接起来
非递归代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| bool insert(const K &key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node *cur = _root;
Node *parent = nullptr;
while (cur)
{
parent = cur;
if (cur->_key > key)
{
cur = cur->left;
}
else if (cur->_key < key)
{
cur = cur->right;
}
else
{
return false;
}
}
Node *new_node = new Node(key);
if (parent->_key > key)
{
parent->left = new_node;
}
else
{
parent->right = new_node;
}
return true;
}
|
递归代码
重点是参数列表的引用
如果走到了root为空,说明到了该插入的位置,现在的root就是上一层父亲左孩子或者右孩子那个指针的别名
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| bool _insert_r(Node *&root, const K &key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key > key)
{
return _insert_r(root->left, key);
}
else if (root->_key < key)
{
return _insert_r(root->right, key);
}
else
{
return false;
}
}
|
遍历
提供一个inorder的接口,调用_inorder()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public:
void inorder()
{
_inorder(_root);
cout << endl;
}
private:
void _inorder(Node *root)
{
if (root == nullptr)
{
return;
}
_inorder(root->left);
cout << root->_key << " ";
_inorder(root->right);
}
|
删除
情况1、左右孩子都为空
可以记录父亲的值,直接干掉当前节点,判断当前节点是父亲的左还是右,然后用空替代当前节点
情况1可以归为情况2的特例
情况2、左右孩子有一个为空
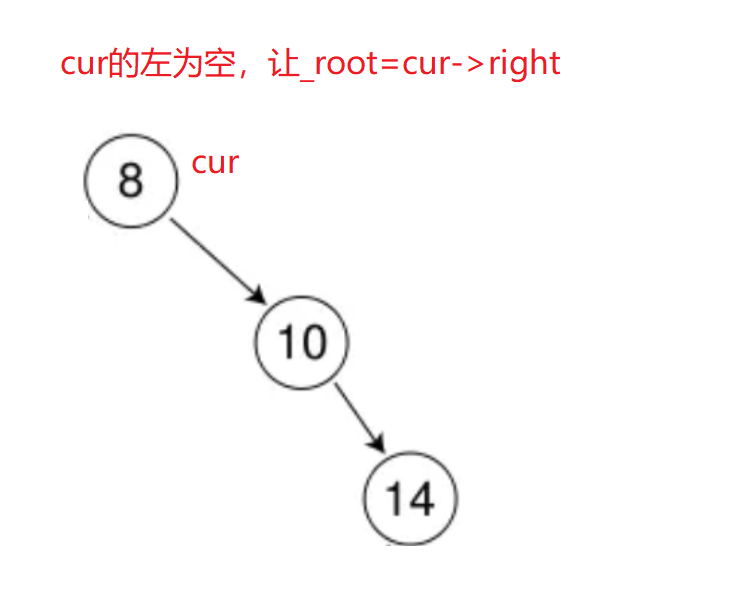
左孩子为空
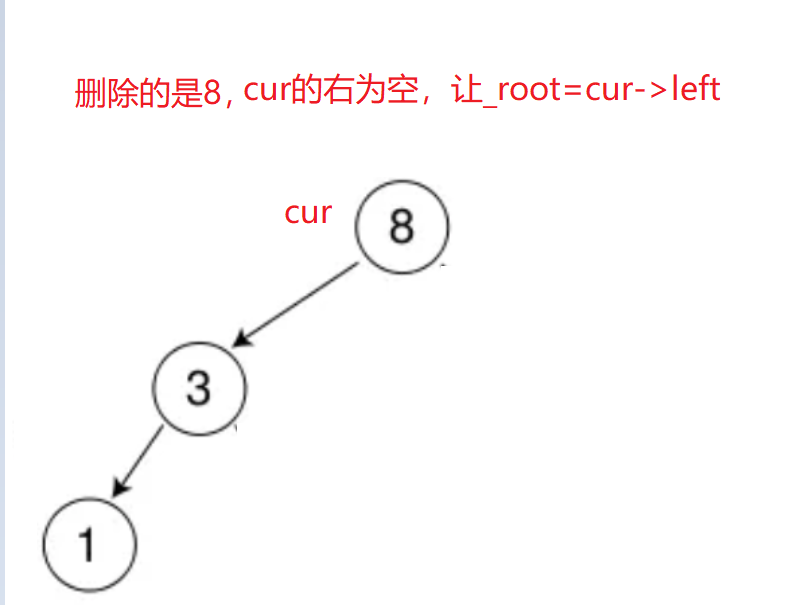
删除的是根
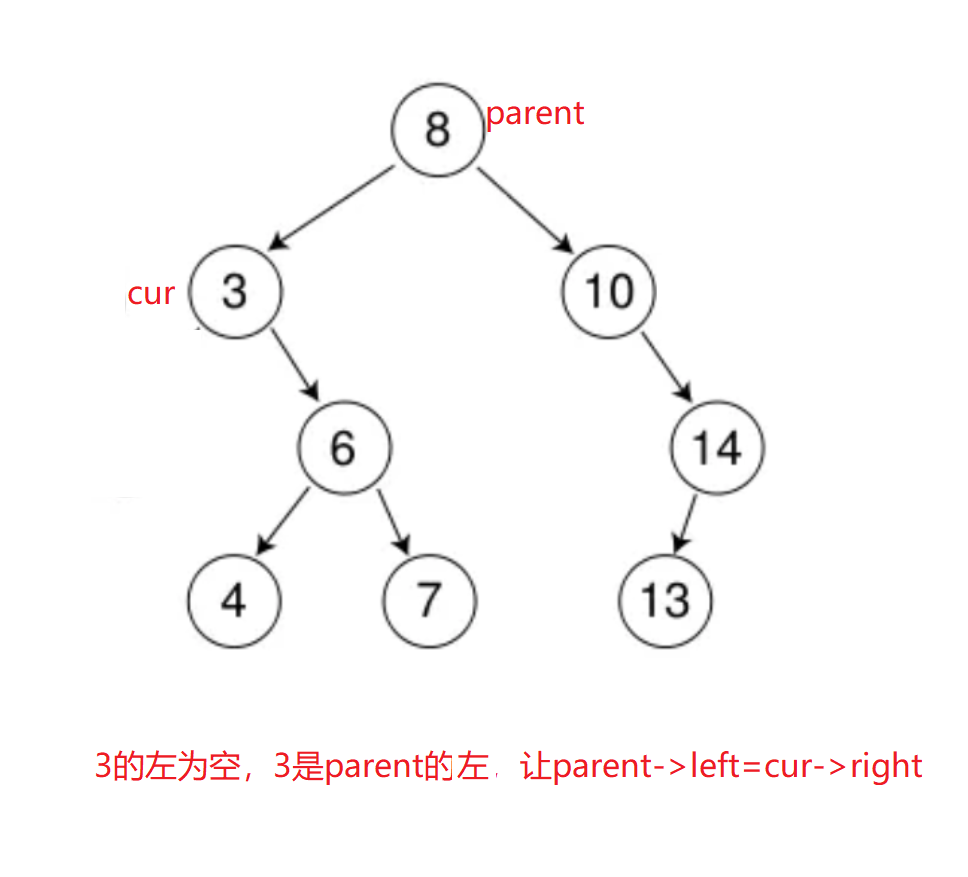
删除的不是根,依然两种情况,主要看这个要删除的节点是父亲的左还是右
如果是父亲的左,就把cur的右给父亲的左
如果是父亲的右,就把cur的右给父亲的右
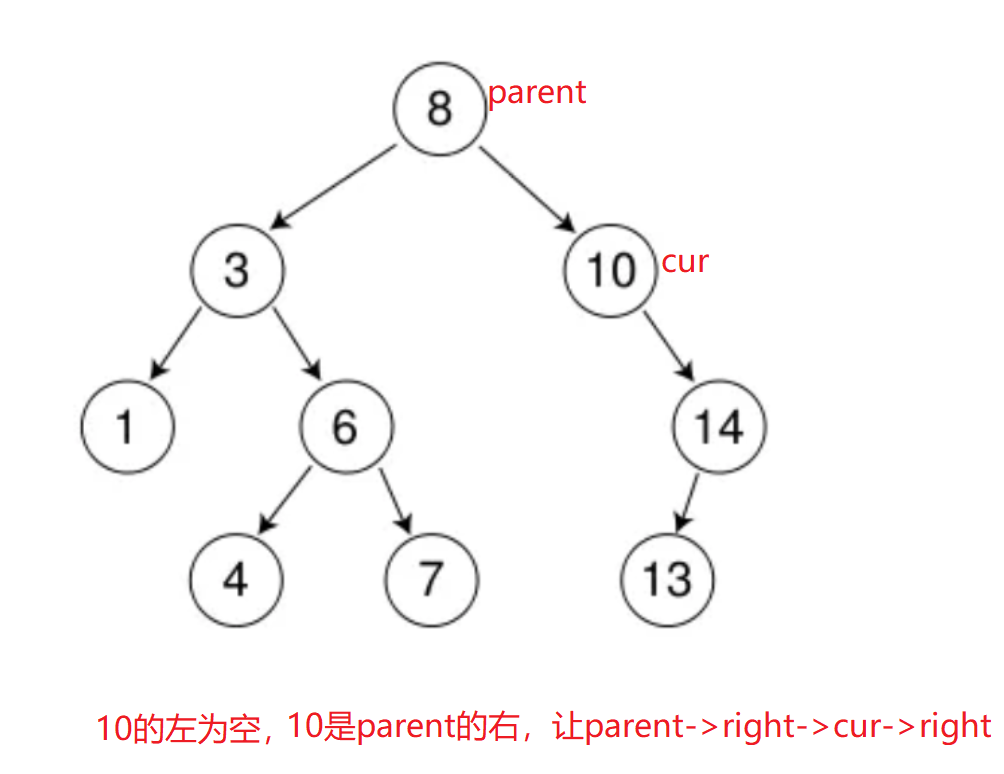
右孩子为空
先判断特殊情况,删除的节点为根节点
其他情况与左孩子为空情况大概相同
- 如果,cur为父亲的左,那么让父亲的左,指向cur的左
- 如果,cur为父亲的右,那么让父亲的右,指向cur的右
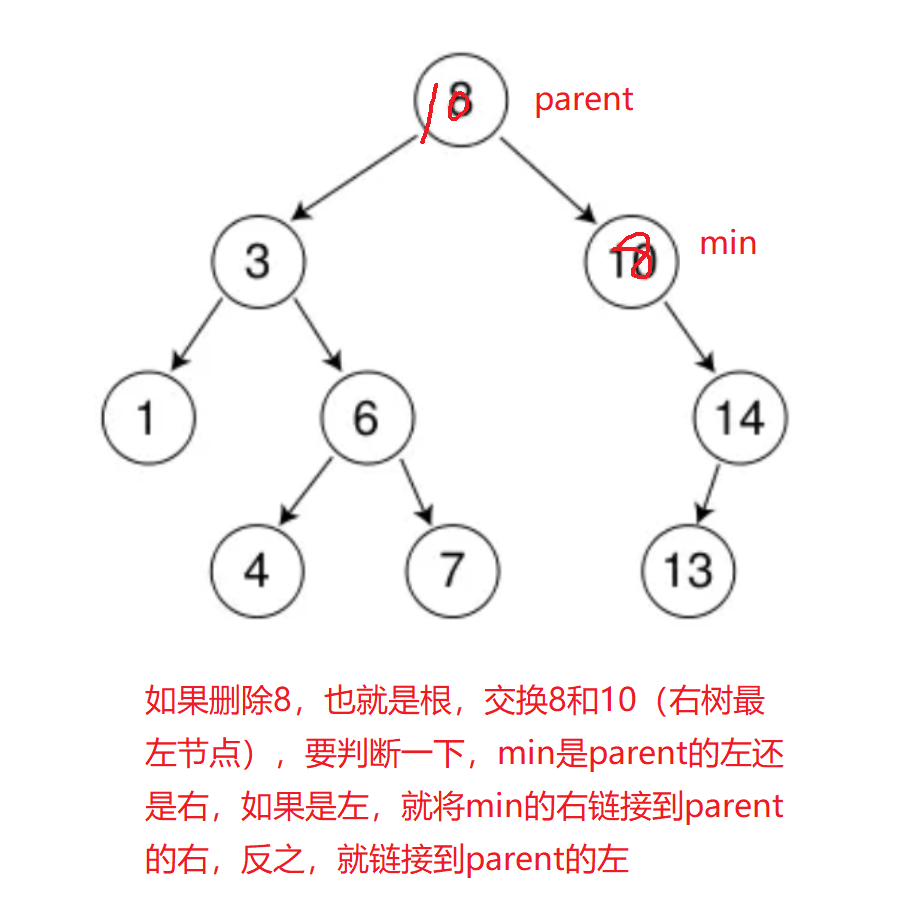
情况3、左右孩子都不为空
- 找右树的最小节点,也就是右树的最左
- 找左树的最大节点 ,也就是左树的最右
情况1

情况2
非递归代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
| bool erase(const K &key)
{
if (_root == nullptr)
return false;
Node *cur = _root;
Node *parent = nullptr;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->right;
}
else
{
if (cur->left == nullptr)
{
if (cur == _root)
{
_root = cur->right;
}
else
{
if (parent->left == cur)
{
parent->left = cur->right;
}
else
{
parent->right = cur->right;
}
}
delete cur;
}
else if (cur->right == nullptr)
{
if (cur == _root)
{
_root = cur->left;
}
else
{
if (parent->left == cur)
{
parent->left = cur->left;
}
else
{
parent->right = cur->left;
}
}
delete cur;
}
else
{
Node *parent = cur;
Node *min = cur->right;
while (min->left)
{
parent = min;
min = min->left;
}
std::swap(min->_key, cur->_key);
if (parent->left == min)
{
parent->left = min->right;
}
else
{
parent->right = min->right;
}
delete min;
}
return true;
}
}
return false;
}
|
递归代码
过程:
- 如果根为空,返回false
- 如果当前值大于key,递归删除左
- 如果当前值小于key,递归删除右
- 如果相等,则进入删除逻辑
分三种情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| bool _erase_r(Node *&root, const K &key)
{
if (root == nullptr)
{
return false;
}
if (root->_key > key)
{
return _erase_r(root->left, key);
}
else if (root->_key < key)
{
return _erase_r(root->right, key);
}
else
{
Node *del = root;
if (root->left == nullptr)
{
root = root->right;
}
else if (root->right == nullptr)
{
root = root->left;
}
else
{
Node *min = root->right;
while (min)
{
min = min->left;
}
std::swap(min->_key, root->_key);
return _erase_r(root->right, key);
}
delete del;
return true;
}
}
|
查找
非递归代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| bool find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
|
递归代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| bool _find_r(Node *root, const K &key)
{
if (root == nullptr)
{
return false;
}
if (root->_key > key)
{
return _find_r(root->left, key);
}
else if (root->_key < key)
{
return _find_r(root->right, key);
}
else
{
return true;
}
}
|