位图

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中？

遍历，时间复杂度O(N)
排序(O(NlogN))，利用二分查找: logN
位图解决

位图概念

所谓位图，就是用每一个比特位来存放某种状态，适用于海量数据，数据无重复的场景。通常是用来判断某个数据存不存在的

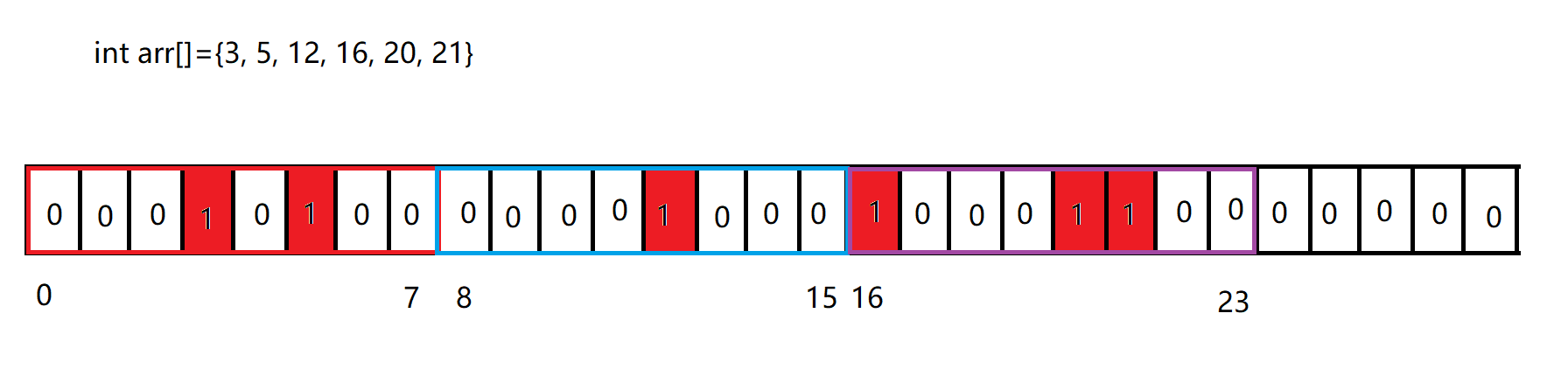
位图实现

这里底层用了vector，存char类型，一个char占8个比特位。然后提供set接口，说明如下：

先找要映射的数据在第几个char：x/8
再看是在char的第几个位：x%8

template<size_t N>
class bitset
{
public:
	bitset()
	{
		_bits.resize(N / 8 + 1, 0);
	}
	void set(size_t x)
	{
		size_t i = x / 8; //找第几个char
		size_t j = x % 8; //第几个char的第几个位
		_bits[i] |= (1 << j);
	}
	void reset(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;
		_bits[i] &= ~(1 << j);
	}

	bool test(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;
		return _bits[i] & (1 << j);
	}
private:
	vector<char> _bits;
};

位图应用

快速查找某个数据是否在一个集合中
排序 + 去重
求两个集合的交集、并集等
操作系统中磁盘块标记

几个例子：

给定100亿个整数，设计算法找到只出现一次的整数？

可以用两个位图，建立kv模型，具体如下：

kv的统计次数搜索模型

0次：00
1次：01
2次及以上：10

template<size_t N>
class twobitset
{
public:
	void set(size_t x)
	{
		bool inset1 = _bs1.test(x);
		bool inset2 = _bs2.test(x);

		//00
		if (inset1 == false && inset2 == false)
		{
			_bs2.set(x);
		}
		else if (inset1 == false && inset2 == true) //01
		{
			_bs1.set(x);
			_bs2.reset(x);
		}
		else if (inset1 == true && inset2 == false) //10
		{
			//11
			_bs1.set(x);
			_bs2.set(x);
		}
	}


	void print_once_num()
	{
		for (size_t i = 0; i < N; ++i)
		{
			//01
			if (_bs1.test(i) == false && _bs2.test(i) == true)
			{
				cout << i << endl;
			}
		}
	}
private:
	bitset<N>_bs1;
	bitset<N>_bs2;
};

给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件的交集？
两个位图

1G=1024Mb
1024MB=1024*1024KB
1024*1024KB=1024*1024*1024Byte
2^30， 约等于10亿Byte

那么100亿整数，就是400亿字节，也就是40G的空间，但是整数的范围就42亿多，那么假设43亿个整数，也就需要43亿个比特位，也就是43亿/8个字节，也就是5亿多字节，大概在0.5G多，可以先依次读取第一个文件中的所有整数，将其映射到一个位图。再读取另一个文件中的所有整数，判断在不在位图中，在就是交集，不在就不是交集。

位图应用变形：一个文件有100亿个int，1G内存，设计算法找到次数不超过两次的所以整数

0次：00
1次：01
2次：10
3次及以上：11

位图特点：

快、节省空间，直接定址法，不存在冲突
相对局限，只能映射整形

布隆过滤器

概念

布隆过滤器是由布隆（Burton Howard Bloom）在1970年提出的一种紧凑型的、比较巧妙的概率型数据结构，特点是高效地插入和查询，可以用来告诉你 “某样东西一定不存在或者可能存在”，它是用多个哈希函数，将一个数据映射到位图结构中。此种方式不仅可以提升查询效率，也可以节省大量的内存空间

用处

1、可以做黑名单查询，不在黑名单的人一定占大多数，如果不在直接返回，如果在，这个结果可能就不准，继续在从数据库中查询。

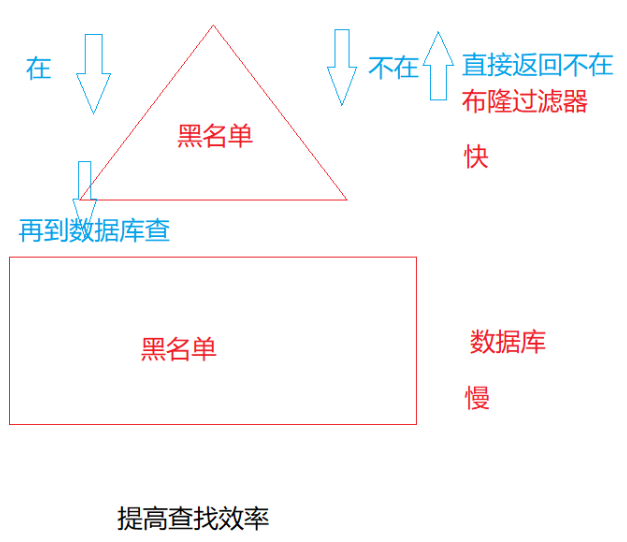
2、注册昵称的场景，如果要注册的昵称不存在，直接注册，如果存在，直接提示（可能有误判）

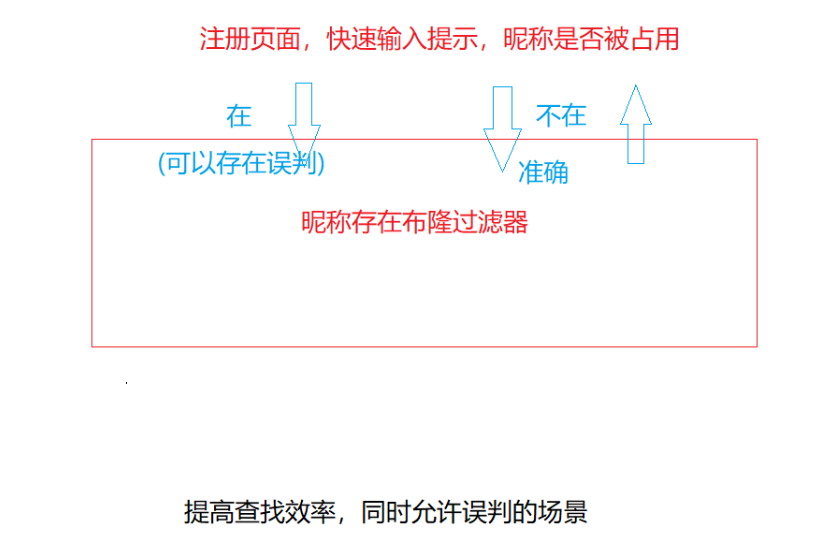
布隆过滤器实现

字符串哈希算法转成整形去映射一个或者多个位置进行标记

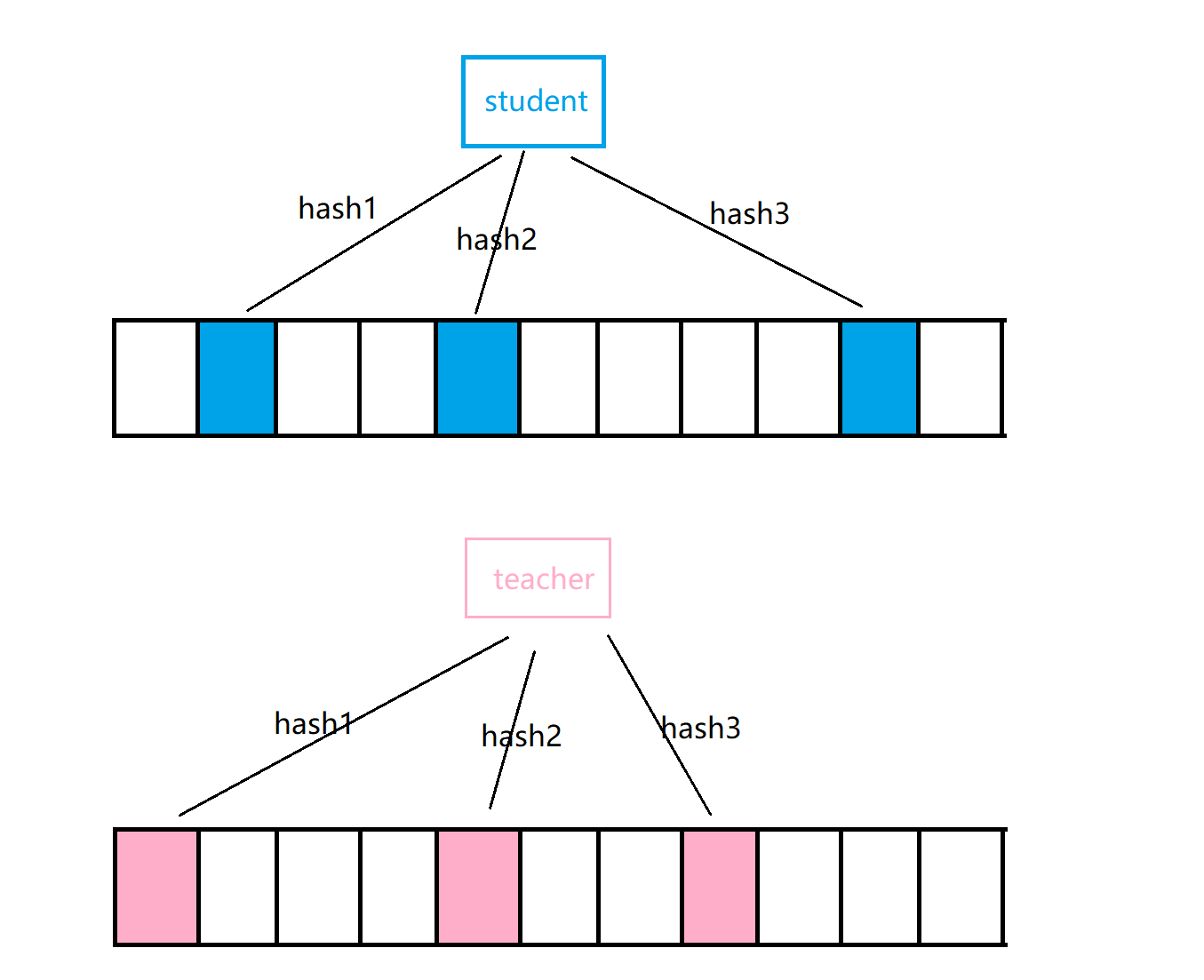
下边为布隆过滤器代码，首先确定m的个数，下边m=5倍的n

k为哈希函数的个数，m为布隆过滤器长度，n为插入元素的个数，p为误报率

struct HashBKDR
{
	// BKDR
	size_t operator()(const string& key)
	{
		size_t val = 0;
		for (auto ch : key)
		{
			val *= 131;
			val += ch;
		}

		return val;
	}
};

struct HashAP
{
	// BKDR
	size_t operator()(const string& key)
	{
		size_t hash = 0;
		for (size_t i = 0; i < key.size(); i++)
		{
			if ((i & 1) == 0)
			{
				hash ^= ((hash << 7) ^ key[i] ^ (hash >> 3));
			}
			else
			{
				hash ^= (~((hash << 11) ^ key[i] ^ (hash >> 5)));
			}
		}
		return hash;
	}
};

struct HashDJB
{
	// BKDR
	size_t operator()(const string& key)
	{
		size_t hash = 5381;
		for (auto ch : key)
		{
			hash += (hash << 5) + ch;
		}

		return hash;
	}
};


// N表示准备要映射N个值

template<size_t N, class K = string, class Hash1 = HashBKDR, class Hash2=HashAP, class Hash3=HashDJB>

class BloomFilter
{
public:
	void Set(const K& key)
	{
		size_t hash1 = Hash1()(key) % (_ratio * N);
		_bits->set(hash1);

		size_t hash2 = Hash2()(key) % (_ratio * N);
		_bits->set(hash2);

		size_t hash3 = Hash3()(key) % (_ratio * N);
		_bits->set(hash3);

	}

	bool Test(const K& key)
	{
		size_t hash1 = Hash1()(key) % (_ratio * N);
		if (_bits->test(hash1) == false)
			return false;

		size_t hash2 = Hash2()(key) % (_ratio * N);
		if (_bits->test(hash2) == false)
			return false;

		size_t hash3 = Hash3()(key) % (_ratio * N);
		if (_bits->test(hash3) == false)
			return false;

		return true;
	}
private:
	const static size_t _ratio = 5;
	std::bitset<_ratio* N>* _bits = new std::bitset<_ratio* N>;
};

几个例子

1、给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件的交集？（近似算法）

先读取其中一个文件当中的query，将其全部映射到一个布隆过滤器当中。
然后读取另一个文件当中的query，依次判断每个query是否在布隆过滤器当中，如果在则是交集，不在则不是交集。（这里的在可能会误判）

2、如何扩展BloomFilter使得它支持删除操作

一般布隆过滤器删除可能会影响其他的元素，因为哈希函数可能会映射到相同的位，如果要支持删除操作，在底层继续增加位图，做引用计数的功能，但是会浪费很多空间，所以布隆过滤器一般不支持删除操作。

哈希切割

1、给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件的交集？（精确算法）

首先需要估算一下这里一个文件的大小，便于确定将一个文件切分为多少个小文件。
假设平均每个query为20字节，那么100亿个query就是200G，由于我们只有1G内存，这里可以考虑将一个文件切分成400个小文件。
这里我们将这两个文件分别叫做A文件和B文件，此时我们将A文件切分成了A0~A399共400个小文件，将B文件切分成了B0~B399共400个小文件。

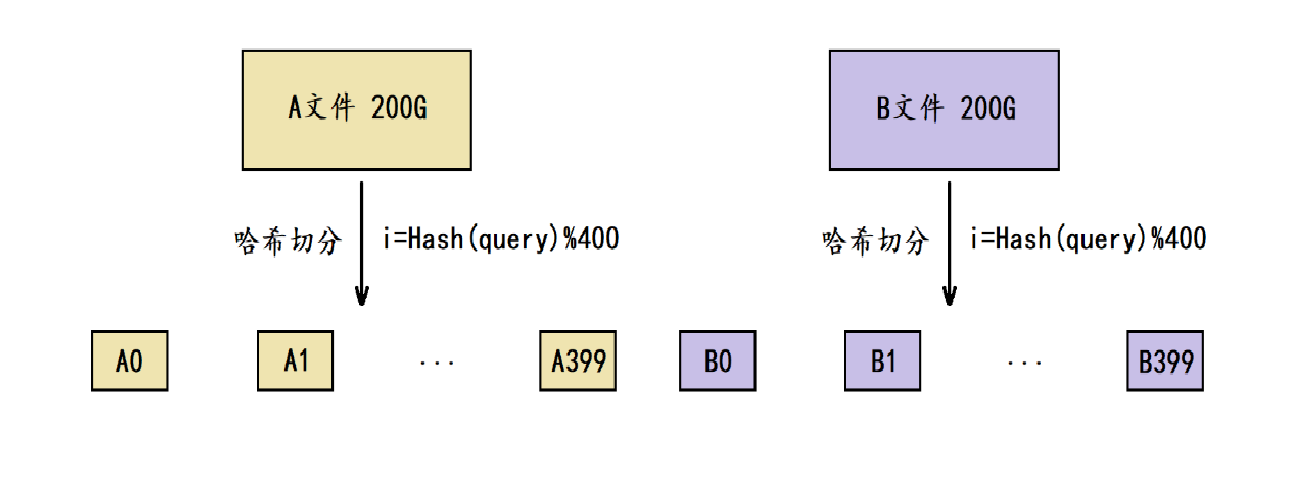
依次读取文件A中query，i=Hash(query)%400，这个query进入Ai号小文件，相同的query一定进入编号相同的小文件

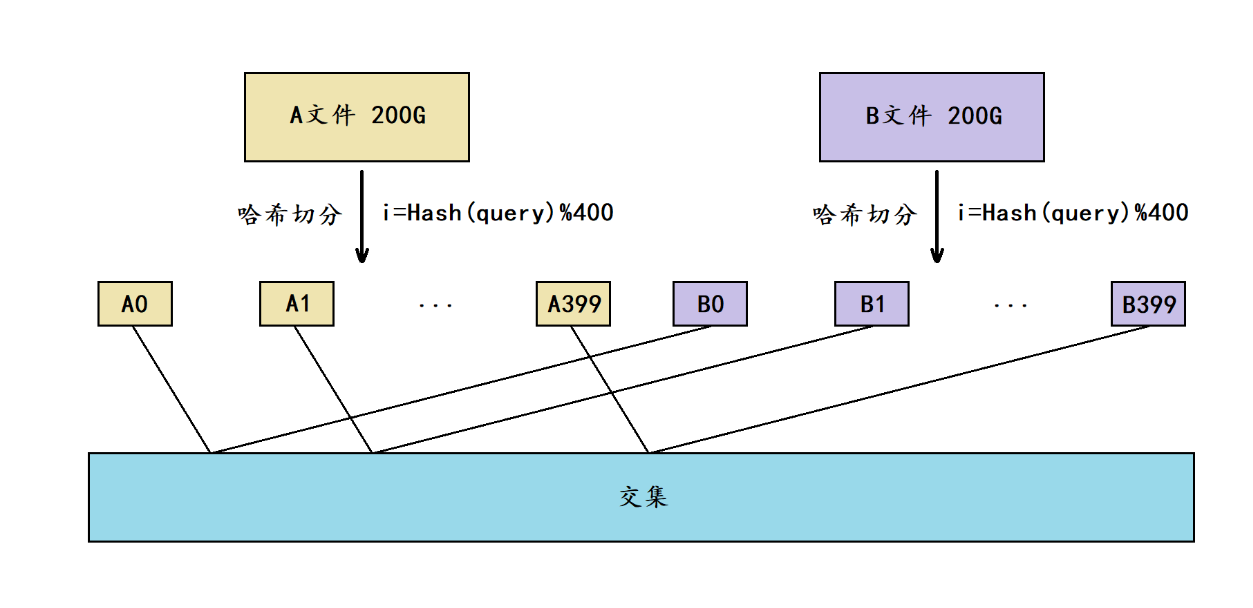
经过切分后理论上每个小文件的平均大小是512M，因此我们可以将其中一个小文件加载到内存，并放到一个set容器中，再遍历另一个小文件当中的query，依次判断每个query是否在set容器中，如果在则是交集，不在则不是交集。
当哈希切分并不是平均切分，有可能切出来的小文件中有一些小文件的大小仍然大于1G，此时如果与之对应的另一个小文件可以加载到内存，则可以选择将另一个小文件中的query加载到内存，因为我们只需要将两个小文件中的一个加载到内存中就行了。
但如果两个小文件的大小都大于1G，那我们可以考虑将这两个小文件再进行一次切分，将其切成更小的文件，方法与之前切分A文件和B文件的方法类似。

2、给一个超过100G大小的log file，log中存着IP地址，设计算法找到出现次数最多的IP地址？与上题条件相同，如何找到top K的IP

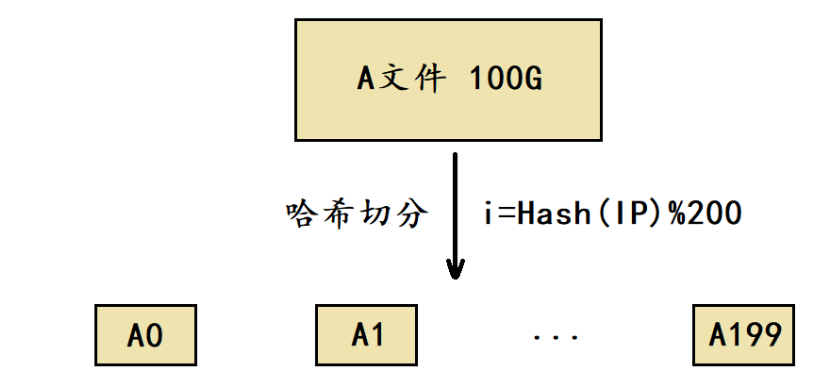
相同的IP一定进入同一个小文件，然后依次使用map<string,int>对每个小文件统计次数

TopK，建立一个K值为<ip, count>的小堆。依次加载每个文件，如果某个IP地址出现的次数大于堆顶IP地址出现的次数，则将该IP地址与堆顶的IP地址进行交换，然后再进行一次向下调整，使其仍为小堆，最终比对完所有小文件中的IP地址后，这个小堆当中的K个IP地址就是出现次数top K的IP地址。