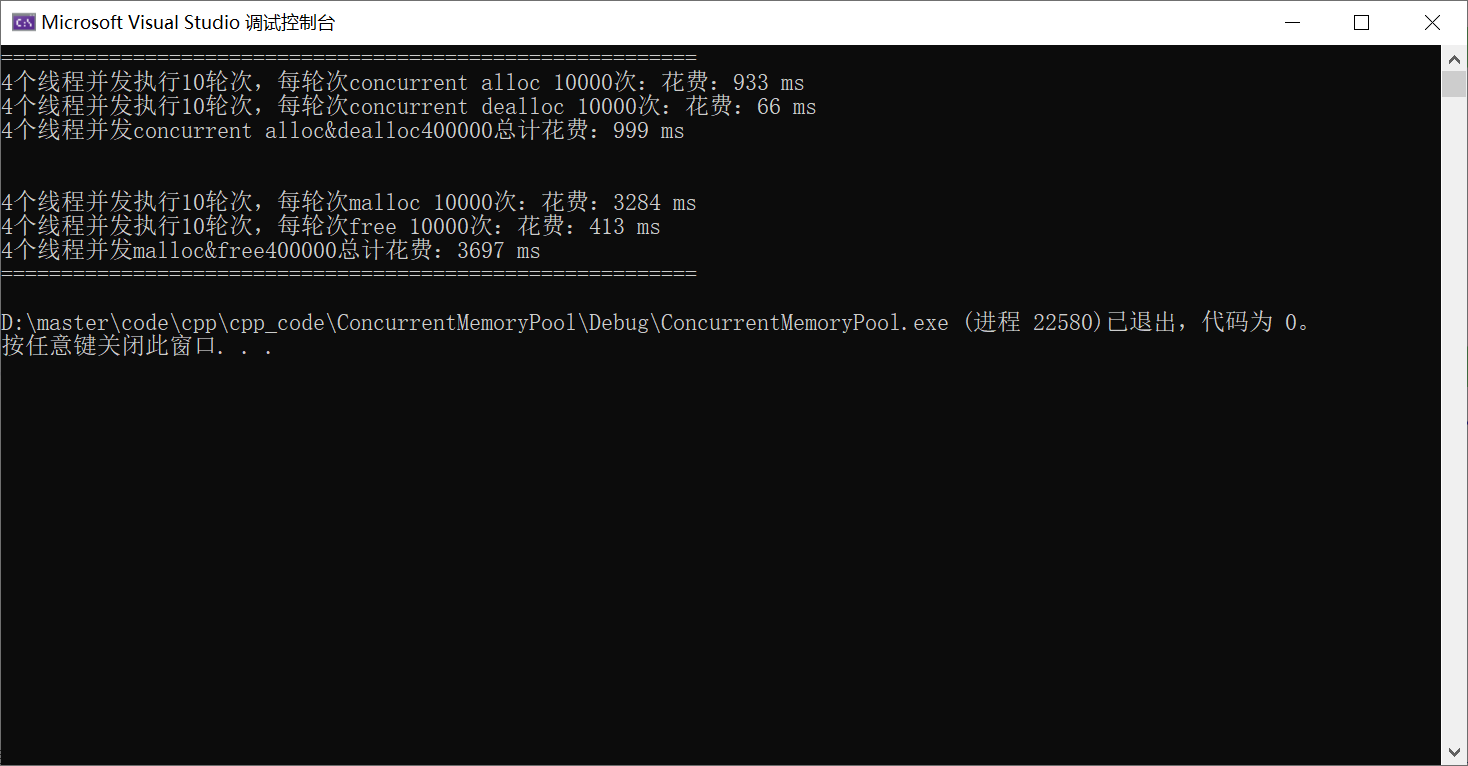
多线程环境下对比malloc测试

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
#include"ConcurrentAlloc.h"

// ntimes 一轮申请和释放内存的次数
// rounds 轮次
void BenchmarkMalloc(size_t ntimes, size_t nworks, size_t rounds)
{
	std::vector<std::thread> vthread(nworks);
	std::atomic<size_t> malloc_costtime = 0;
	std::atomic<size_t> free_costtime = 0;

	for (size_t k = 0; k < nworks; ++k)
	{
		vthread[k] = std::thread([&, k]() {
			std::vector<void*> v;
			v.reserve(ntimes);

			for (size_t j = 0; j < rounds; ++j)
			{
				size_t begin1 = clock();
				for (size_t i = 0; i < ntimes; i++)
				{
					//v.push_back(malloc(16));
					v.push_back(malloc((16 + i) % 8192 + 1));
				}
				size_t end1 = clock();

				size_t begin2 = clock();
				for (size_t i = 0; i < ntimes; i++)
				{
					free(v[i]);
				}
				size_t end2 = clock();
				v.clear();

				malloc_costtime += (end1 - begin1);
				free_costtime += (end2 - begin2);
			}
			});
	}

	for (auto& t : vthread)
	{
		t.join();
	}


	cout << nworks << "个线程并发执行" << rounds << "轮次，每轮次malloc " << ntimes << "次：花费：" << malloc_costtime << " ms" << endl;


	cout << nworks << "个线程并发执行" << rounds << "轮次，每轮次free " << ntimes << "次：花费：" << free_costtime << " ms" << endl;

	cout << nworks << "个线程并发malloc&free" << nworks * rounds * ntimes << "总计花费：" << malloc_costtime + free_costtime << " ms" << endl;

}


// 单轮次申请释放次数 线程数 轮次
void BenchmarkConcurrentMalloc(size_t ntimes, size_t nworks, size_t rounds)
{
	std::vector<std::thread> vthread(nworks);
	std::atomic<size_t> malloc_costtime = 0;
	std::atomic<size_t> free_costtime = 0;

	for (size_t k = 0; k < nworks; ++k)
	{
		vthread[k] = std::thread([&]() {
			std::vector<void*> v;
			v.reserve(ntimes);

			for (size_t j = 0; j < rounds; ++j)
			{
				size_t begin1 = clock();
				for (size_t i = 0; i < ntimes; i++)
				{
					//v.push_back(ConcurrentAlloc(16));
					v.push_back(ConcurrentAlloc((16 + i) % 8192 + 1));
				}
				size_t end1 = clock();

				size_t begin2 = clock();
				for (size_t i = 0; i < ntimes; i++)
				{
					ConcurrentFree(v[i]);
				}
				size_t end2 = clock();
				v.clear();

				malloc_costtime += (end1 - begin1);
				free_costtime += (end2 - begin2);
			}
			});
	}

	for (auto& t : vthread)
	{
		t.join();
	}


	cout << nworks << "个线程并发执行" << rounds << "轮次，每轮次concurrent alloc " << ntimes << "次：花费：" << malloc_costtime << " ms" << endl;

	cout << nworks << "个线程并发执行" << rounds << "轮次，每轮次concurrent dealloc " << ntimes << "次：花费：" << free_costtime << " ms" << endl;

	cout << nworks << "个线程并发concurrent alloc&dealloc" << nworks * rounds * ntimes << "总计花费：" << malloc_costtime + free_costtime << " ms" << endl;

}

int main()
{
	size_t n = 10000;
	cout << "==========================================================" << endl;
	BenchmarkConcurrentMalloc(n, 4, 10);
	cout << endl << endl;

	BenchmarkMalloc(n, 4, 10);
	cout << "==========================================================" << endl;

	return 0;
}

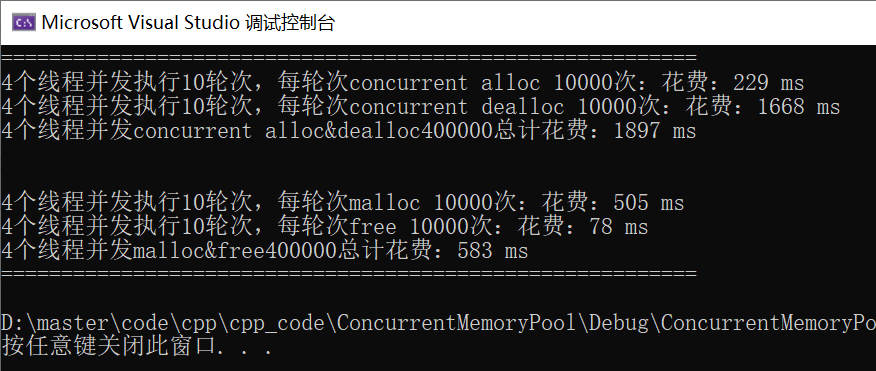
申请释放固定内存大小

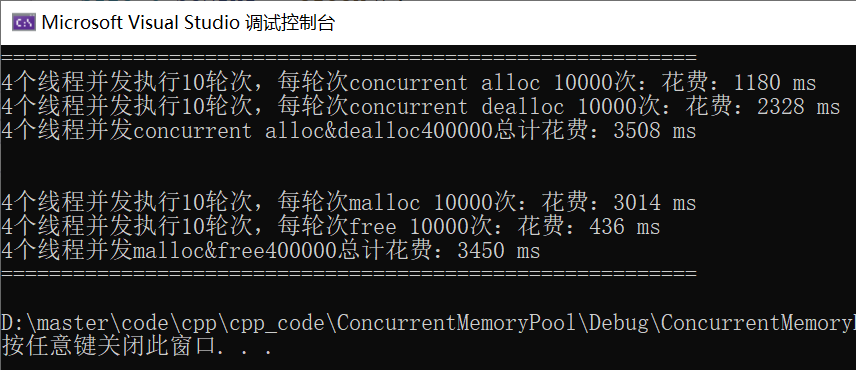
image.png

申请释放不同内存大小

image.png

性能瓶颈分析

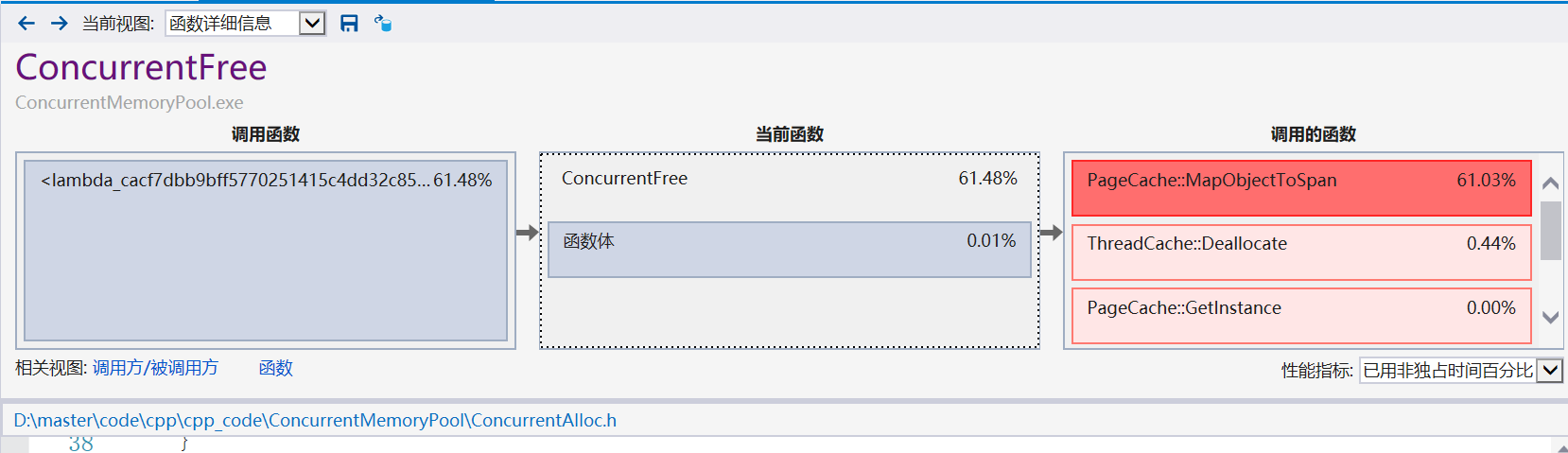
上述测试发现，我们的内存池比malloc还是差一些的，但是不大容易知道到底是代码的哪一个部分消耗的性能较多，不知道性能的瓶颈在哪里，这时候可以使用性能分析工具

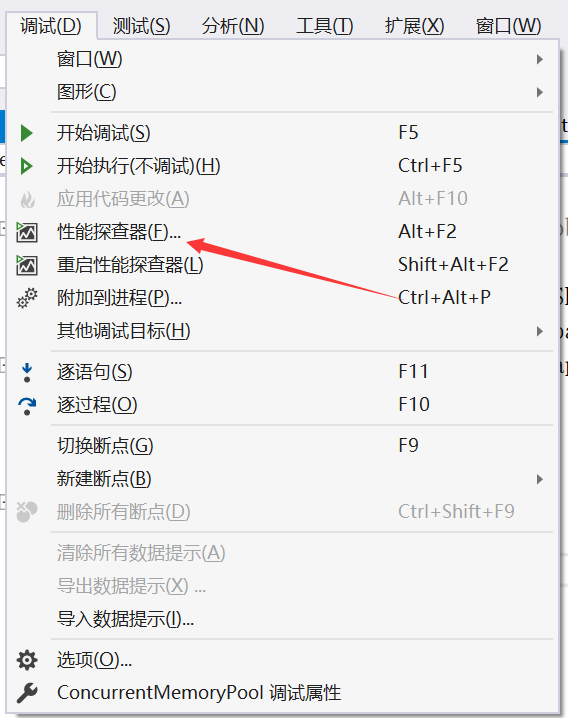
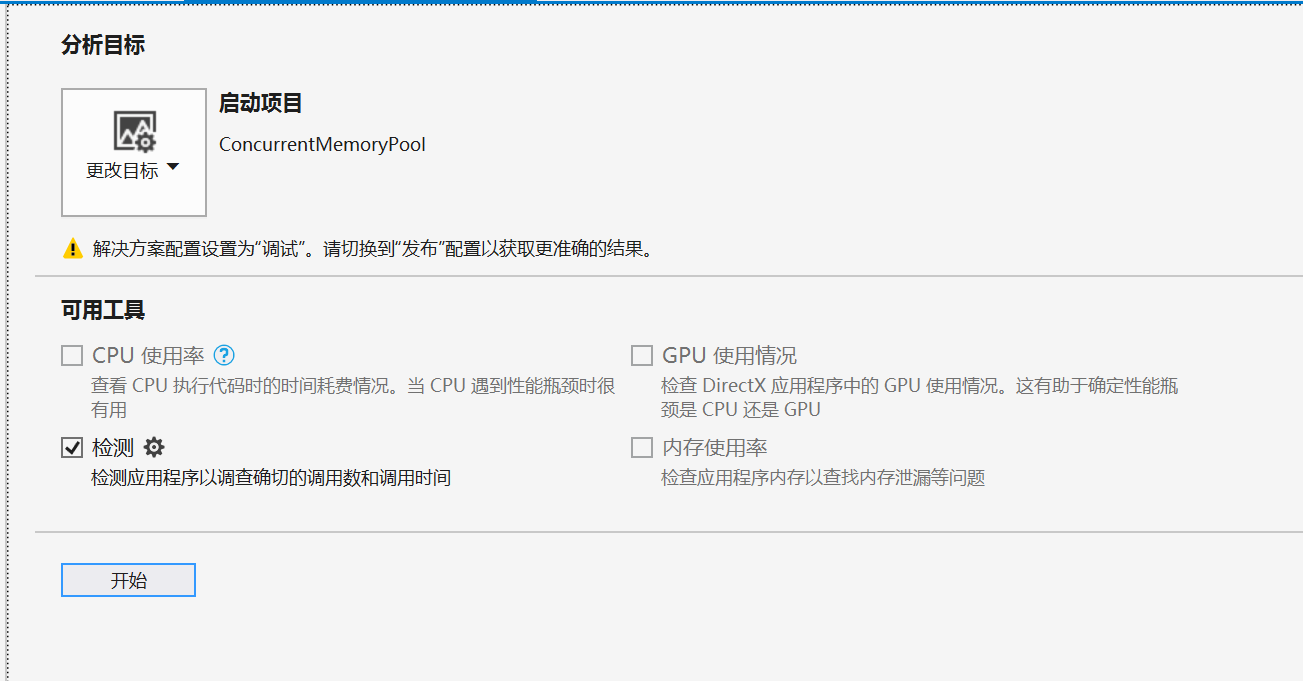
image.png

打开性能探查器，可用工具类，检测项打上对号

image.png

点击开始

image.png

可以发现MapObjectToSpan所花费时间非常长，因为涉及到锁的竞争问题，那么我们应该如何进行优化呢？

基数树优化

这里使用基数树进行优化，基数树实际是一个分层的哈希表，根据所分层数，可以分为单层基数树、二层基数树、三层基数树

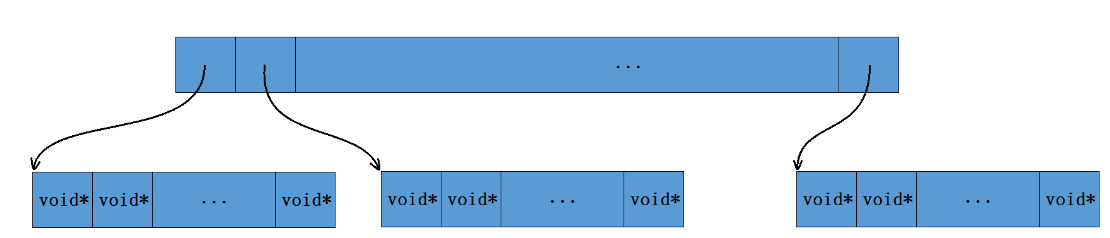
单层基数树

单层基数树使用的是直接定址法，在32位平台下，最多分成2^32/2^13次方个页，我们直接开2^(31-13)次方大小的数组

这这里可以用非类型模板参数，将次方传入，1<< BITS 就是2的BITS次方。直接开这么长的数组

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
template <int BITS>
class TCMalloc_PageMap1 {
private:
	static const int LENGTH = 1 << BITS;
	void** array_;

public:
	typedef uintptr_t Number;

	//explicit TCMalloc_PageMap1(void* (*allocator)(size_t)) {
	explicit TCMalloc_PageMap1() {
		//array_ = reinterpret_cast<void**>((*allocator)(sizeof(void*) << BITS));
		size_t size = sizeof(void*) << BITS;
		size_t alignSize = SizeClass::_RoundUp(size, 1 << PAGE_SHIFT);
		array_ = (void**)SystemAlloc(alignSize >> PAGE_SHIFT);
		memset(array_, 0, sizeof(void*) << BITS);
	}

	// Return the current value for KEY.  Returns NULL if not yet set,
	// or if k is out of range.
	void* get(Number k) const {
		if ((k >> BITS) > 0) {
			return NULL;
		}
		return array_[k];
	}

	// REQUIRES "k" is in range "[0,2^BITS-1]".
	// REQUIRES "k" has been ensured before.
	//
	// Sets the value 'v' for key 'k'.
	void set(Number k, void* v) {
		array_[k] = v;
	}
};

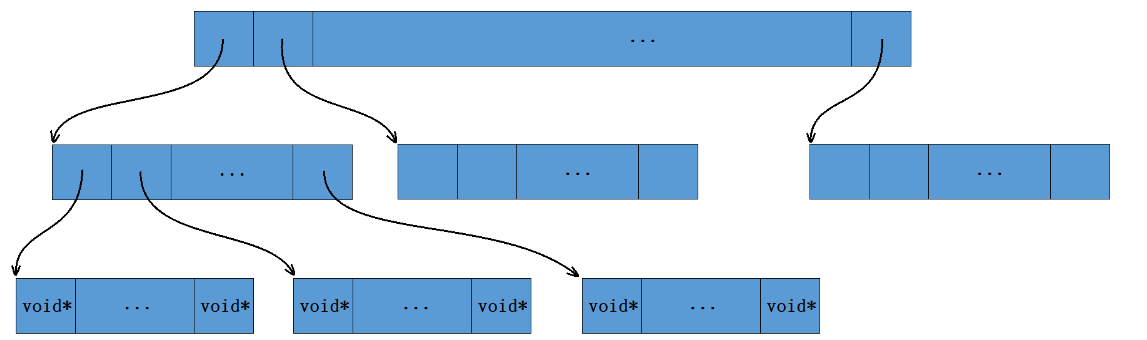
二层基数树

假设同样在32位平台下，最多分成2^32/2^13 = 2^19次方个页，最多用19个比特位可以标识，用二层得基数树，第一层只用5个比特位，做直接定址，对应的下标存的元素是 void* values[LEAF_LENGTH]，剩下的14位可以总共映射 length = 1<<14个数据

image.png

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
// Two-level radix tree
template <int BITS>
class TCMalloc_PageMap2 {
private:
	// Put 32 entries in the root and (2^BITS)/32 entries in each leaf.
	static const int ROOT_BITS = 5; //第一层对应页号的前5个比特位
	static const int ROOT_LENGTH = 1 << ROOT_BITS; //第一层存储元素的个数 2^5


	static const int LEAF_BITS = BITS - ROOT_BITS;//第二层对应页号的其余比特位 19-5=14
	static const int LEAF_LENGTH = 1 << LEAF_BITS; //第二层存储元素的个数 2^14
	// Leaf node
	struct Leaf {
		void* values[LEAF_LENGTH];
	};

	Leaf* root_[ROOT_LENGTH];             // Pointers to 32 child nodes
	void* (*allocator_)(size_t);          // Memory allocator

public:
	typedef uintptr_t Number;

	//explicit TCMalloc_PageMap2(void* (*allocator)(size_t)) {
	explicit TCMalloc_PageMap2() {
		//allocator_ = allocator;
		memset(root_, 0, sizeof(root_));

		PreallocateMoreMemory();
	}

	void* get(Number k) const {
		const Number i1 = k >> LEAF_BITS;  // 右移14位，得到前5位
		const Number i2 = k & (LEAF_LENGTH - 1);
		if ((k >> BITS) > 0 || root_[i1] == NULL) {
			return NULL;
		}
		return root_[i1]->values[i2];
	}

	void set(Number k, void* v) {
		const Number i1 = k >> LEAF_BITS;
		// 1000 0000 0000 000-1 = 0111 1111 1111 11
		// 相与获得后14位
		const Number i2 = k & (LEAF_LENGTH - 1); 
		ASSERT(i1 < ROOT_LENGTH);
		root_[i1]->values[i2] = v;
	}

	// 确保映射[start ， start+n-1]页号的空间是开好的
	bool Ensure(Number start, size_t n) {
		for (Number key = start; key <= start + n - 1;) {
			const Number i1 = key >> LEAF_BITS;

			// Check for overflow
			if (i1 >= ROOT_LENGTH)
				return false;

			// Make 2nd level node if necessary
			if (root_[i1] == NULL) {
				//Leaf* leaf = reinterpret_cast<Leaf*>((*allocator_)(sizeof(Leaf)));
				//if (leaf == NULL) return false;
				static ObjectPool<Leaf>	leafPool;
				Leaf* leaf = (Leaf*)leafPool.New();

				memset(leaf, 0, sizeof(*leaf));
				root_[i1] = leaf;
			}

			// Advance key past whatever is covered by this leaf node
			key = ((key >> LEAF_BITS) + 1) << LEAF_BITS;
		}
		return true;
	}

	void PreallocateMoreMemory() {
		// 将第二层全部的空间都开好
		Ensure(0, 1 << BITS);
	}
};

在32位平台下，第一层数组占，2^5* 4=2^7字节，第二层最多有2^5^2^14^4=2^21=2M，消耗也不大，可以直接全开出来

三层基数树

64位平台下，公共有2^64/2^13=2^51个页，一层基数树肯定不行，二层页不大行，用三层基数树，三层基数树就是将存储页号的比特位分三次映射

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
// Three-level radix tree
template <int BITS>
class TCMalloc_PageMap3
{
private:
	static const int INTERIOR_BITS = (BITS + 2) / 3;       //第一、二层对应页号的比特位个数
	static const int INTERIOR_LENGTH = 1 << INTERIOR_BITS; //第一、二层存储元素的个数
	static const int LEAF_BITS = BITS - 2 * INTERIOR_BITS; //第三层对应页号的比特位个数
	static const int LEAF_LENGTH = 1 << LEAF_BITS;         //第三层存储元素的个数
	struct Node
	{
		Node* ptrs[INTERIOR_LENGTH];
	};
	struct Leaf
	{
		void* values[LEAF_LENGTH];
	};
	Node* NewNode()
	{
		static ObjectPool<Node> nodePool;
		Node* result = nodePool.New();
		if (result != NULL)
		{
			memset(result, 0, sizeof(*result));
		}
		return result;
	}
	Node* root_;
public:
	typedef uintptr_t Number;
	explicit TCMalloc_PageMap3()
	{
		root_ = NewNode();
	}
	void* get(Number k) const
	{
		const Number i1 = k >> (LEAF_BITS + INTERIOR_BITS);         //第一层对应的下标
		const Number i2 = (k >> LEAF_BITS) & (INTERIOR_LENGTH - 1); //第二层对应的下标
		const Number i3 = k & (LEAF_LENGTH - 1);                    //第三层对应的下标
		//页号超出范围，或映射该页号的空间未开辟
		if ((k >> BITS) > 0 || root_->ptrs[i1] == NULL || root_->ptrs[i1]->ptrs[i2] == NULL)
		{
			return NULL;
		}
		return reinterpret_cast<Leaf*>(root_->ptrs[i1]->ptrs[i2])->values[i3]; //返回该页号对应span的指针
	}
	void set(Number k, void* v)
	{
		assert(k >> BITS == 0);
		const Number i1 = k >> (LEAF_BITS + INTERIOR_BITS);         //第一层对应的下标
		const Number i2 = (k >> LEAF_BITS) & (INTERIOR_LENGTH - 1); //第二层对应的下标
		const Number i3 = k & (LEAF_LENGTH - 1);                    //第三层对应的下标
		Ensure(k, 1); //确保映射第k页页号的空间是开辟好了的
		reinterpret_cast<Leaf*>(root_->ptrs[i1]->ptrs[i2])->values[i3] = v; //建立该页号与对应span的映射
	}
	//确保映射[start,start+n-1]页号的空间是开辟好了的
	bool Ensure(Number start, size_t n)
	{
		for (Number key = start; key <= start + n - 1;)
		{
			const Number i1 = key >> (LEAF_BITS + INTERIOR_BITS);         //第一层对应的下标
			const Number i2 = (key >> LEAF_BITS) & (INTERIOR_LENGTH - 1); //第二层对应的下标
			if (i1 >= INTERIOR_LENGTH || i2 >= INTERIOR_LENGTH) //下标值超出范围
				return false;
			if (root_->ptrs[i1] == NULL) //第一层i1下标指向的空间未开辟
			{
				//开辟对应空间
				Node* n = NewNode();
				if (n == NULL) return false;
				root_->ptrs[i1] = n;
			}
			if (root_->ptrs[i1]->ptrs[i2] == NULL) //第二层i2下标指向的空间未开辟
			{
				//开辟对应空间
				static ObjectPool<Leaf> leafPool;
				Leaf* leaf = leafPool.New();
				if (leaf == NULL) return false;
				memset(leaf, 0, sizeof(*leaf));
				root_->ptrs[i1]->ptrs[i2] = reinterpret_cast<Node*>(leaf);
			}
			key = ((key >> LEAF_BITS) + 1) << LEAF_BITS; //继续后续检查
		}
		return true;
	}
	void PreallocateMoreMemory()
	{}
};

当需要建立某一页号的映射关系时，先确保存储该页映射的数组空间是开好的，调用Ensure函数，如果没开好，就开辟对应的空间

使用基数树优化

我们在32位平台下测试，直接使用一层基数树即可将unordered_map替换成基数树的结构，并用set和get函数，替换方括号和find的作用

更改代码

1
TCMalloc_PageMap1<32 - PAGE_SHIFT> _idSpanMap;  //32-13=19，总共2^19个页

建立映射：

1
_idSpanMap.set(span->_pageId, span);

读取Span

1
Span* ret = (Span*)_idSpanMap.get(id);

优化原理

基数树的检索可能略好一点，但是最重要的是基数树的结构不需要加锁，map和unordered_map，插入数据底层的数据结构可能会变化，比如红黑树的选择，哈希表的扩容，所以在读取映射关系时需要加锁，但是基数树一旦开好空间就不会发生变化。
我们不会同时对一个页进行读取映射和建立映射的操作，只有在释放对象的时候才需要读取，建立映射都是在page cache中进行，建立映射的对应的span的usecount为0，而读取对应的span的usecount不为0，所以不会对一个页同时进行读取和建立映射。

性能对比

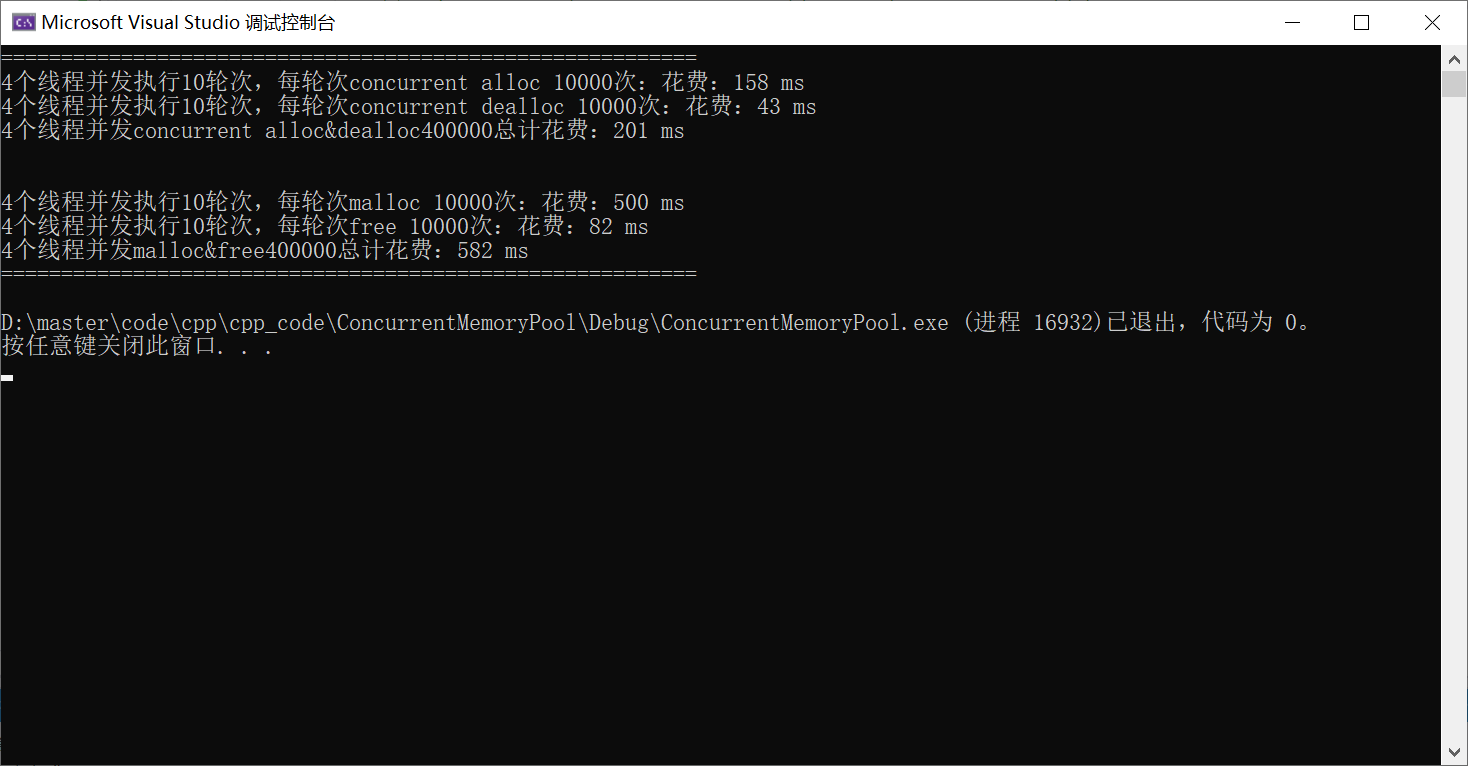
再次与malloc进行对比

固定大小的对象的申请和释放

image.png

不固定大小的对象的申请和释放

image.png

可以看到两种场景，都比malloc快2~3倍左右