C++11(右值)
右值引用和移动语义
传统的C++语法中就有引用的语法,而C++11中新增了的右值引用语法特性,所以从现在开始我们之前学习的引用就叫做左值引用。无论左值引用还是右值引用,都是给对象取别名。
右值引入
在以前我们知道有引用的语法,我们通常叫做左值引用,那么什么是左值呢?可以看下边的几个例子
123456789101112131415161718192021int main(){ // 左值:可以取它的地址 /*int a = 10; const int b = 20; int* p = &a; *p = 100;*/ // 以下的p、b、c、*p都是左值 int* p = new int(0); int b = 1; const int c = 2; // 以下几个是对上面左值的左值引用 int*& rp = p; int& rb = b; const int& rc = c; int& pvalue = *p; double x = 1.1, y = 2.2;}
可以看到,左值,可以获取它的地址+可以对它赋值。当然定义时 ...
C++11基础
列表初始化
{} 初始化
在C++98中,标准允许使用花括号{}对数组或者结构体元素进行统一的列表初始值设定。
比如下方示例:
C++11扩大了用大括号括起的列表(初始化列表)的使用范围,使其可用于所有的内置类型和用户自定义的类型,使用初始化列表时,可添加等号(=),也可不添加
内置类型
以下三种写法一样
自定义类型
对于自定义类型同样适用
12345678910111213141516171819202122232425class Date{public: Date(int year, int month, int day) :_year(year) , _month(month) , _day(day) { cout << "Date(int year, int month, int day)" << endl; }private: int _year; int _month; int _day;};int main(){ // 都是在调用构造函数 Date d1(20 ...
增程式电动汽车CD/CS控制策略
一、简介
CD/CS策略是最简单的EMS控制策略,这是基于规则的,最简单的控制策略,容易在实车上实现,通常在科研中用于与其他策略进行比较来体现其控制策略的优势。
二、优缺点
优点:
实现简单
实时
发动机可工作在高效区
缺点:
适应力差
电池频繁冲放电
三、流程图
四、原理
1、CD模式
需求功率只由电池提供,先推导状态变量SOC,
SO˙C=dSOCdt=−IessCess=UOCV2−4PessRess−UOCV2RessCess S\dot OC=\frac{dSOC}{dt}=\frac{-I_{ess}}{C_{ess}}=\frac{\sqrt{U^2_{OCV}-4P_{ess}R_{ess}}-U_{OCV}}{2R_{ess}C_{ess}}
SO˙C=dtdSOC=Cess−Iess=2RessCessUOCV2−4PessRess−UOCV
SOCmin≤SOC≤maxSOC_{min} \leq SOC\leq_{max}
SOCmin≤SOC≤max
推导SOC的导数(安时计量法)
SOCk+1=SOCk− ...
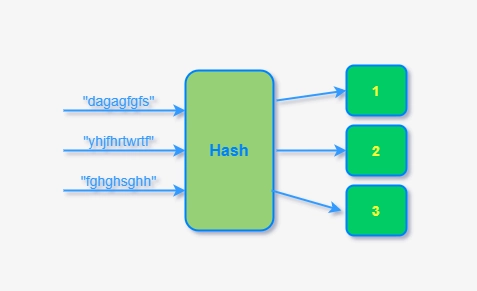
哈希应用
位图
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中?
遍历,时间复杂度O(N)
排序(O(NlogN)),利用二分查找: logN
位图解决
位图概念
所谓位图,就是用每一个比特位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的
位图实现
这里底层用了vector,存char类型,一个char占8个比特位。然后提供set接口,说明如下:
先找要映射的数据在第几个char:x/8
再看是在char的第几个位:x%8
123456789101112131415161718192021222324252627282930template<size_t N>class bitset{public: bitset() { _bits.resize(N / 8 + 1, 0); } void set(size_t x) { size_t i = x / 8; //找第几个char size_t j = x % 8; //第几个char的第几个 ...
哈希
unordered系列关联式容器
内部是无序的,查询很快
几个函数说明:
函数声明
功能介绍
operator[]
返回与key对应的value值
bucket_count()
返回桶的个数
size_t bucket_size(size_t n)const
返回n号桶有效元素的个数
size_t bucket(const K& key)
返回元素key对应的桶号
底层结构
unordered系列的关联式容器之所以效率比较高,是因为其底层使用了哈希结构。
概念
通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立 一一映射的关系,那么在查找时通过该函数可以很快找到该元素。
例如:数据集合{1,7,6,4,5,9}
哈希函数设置为:hash(key) = key % capacity; capacity为存储元素底层空间总的大小
哈希冲突
不同关键字通过相同哈希哈数计算出相同的哈希地址,该种现象称为哈希冲突或哈希碰撞。
哈希函数
引起哈希冲突的一个原因可能是:哈希函数设计不够合理。
哈希函数设计原则:
哈希函数 ...
map和set
关联式容器也是用来存储数据的,与序列式容器不同的是,其里面存储的是<key, value>结构的键值对,在数据检索时比序列式容器效率更高
set
排序+去重
find找不到会返回end
lower_bound(val) 返回大于或者等于val的位置
upper_bound(val) 返回大于val的位置
123456789101112131415161718192021222324252627282930313233343536373839int a[] = { 3,1, 2, 1, 6, 3, 8,3, 5,3};multiset<int> s(a, a + sizeof(a) / sizeof(int));// 排序for (auto e : s){ cout << e << " ";}cout << endl;cout << s.count(1) << endl;// find时,如果有多个值,返回中序的第一个auto pos = s. ...
红黑树
红黑树概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
红黑树的性质
每个结点不是红色就是黑色
根节点是黑色的
如果一个节点是红色的,则它的两个孩子结点是黑色的,树中没有连续的红节点
对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
为什么满足上面的性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径中节点个数的两倍?
极限最短:全黑
极限最长:一黑一红
红黑树结构
123456789101112131415161718192021222324252627282930313233enum Color{ RED, BLACK};template <class K, class V>struct RBTreeNode{ RBTreeNode<K, V&g ...
AVL树
AVL概念
当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
它的左右子树都是AVL树
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在
O(log2n)O(log_2 n)O(log2n),搜索时间复杂度O(log2nlog_2 nlog2n)
AVL操作
插入
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108bool insert(con ...
606. 根据二叉树创建字符串
606. 根据二叉树创建字符串
我的错误思路
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {& ...
236. 二叉树的最近公共祖先
236. 二叉树的最近公共祖先
解法1
规则:
一个是左子树中的节点,一个是右子树中的节点,那么他就是最近的公共祖先
这种做法的时间复杂度是O(H*N),如果公共祖先在很下面,时间复杂度就比较高
每次找高度次
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354class Solution {public: bool Find(TreeNode* root, TreeNode* x) { if(root==nullptr) return false; /*if(root==x) return true; if(Find(root->left, x)) return true; if(Find(root->right,x)) return true; ...